Теорема о равномерном распределении энергии по степеням свободы

До сих пор мы рассматривали одноатомный идеальный газ. Частицы одноатомного газа рассматривались как материальные точки, которые могут совершать только поступательные движения.

Средняя энергия такой частицы полностью определяется средней кинетической энергией ее поступательного движения:

.

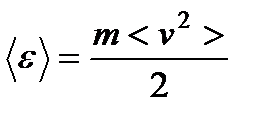Энергию эту можно представить как сумму трех слагаемых — кинетических энергий движения молекулы по трем взаимно перпендикулярным направлениям:

,

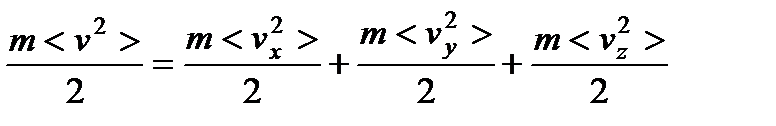где v_x, v_y, v_z – составляющие скорости молекулы по трем осям координат. Полная хаотичность молекулярных движений позволяет считать, что средние значения кинетических энергий по трем направлениям равны друг другу:

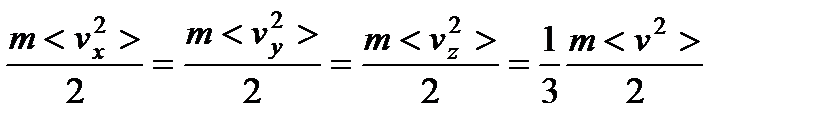. (89)

Так как согласно основному уравнению кинетической теории

,

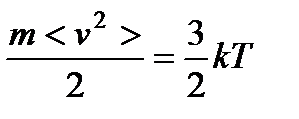то каждое из слагаемых равенства (89) равно .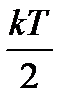

Разделение кинетической энергии частицы на три независимые составляющие связано с тем, что частица рассматривается как свободная материальная точка, обладающая тремя степенями свободы.

Напомним, что числом степеней свободы механической системы называется число независимых координат, определяющих ее положение и конфигурацию в пространстве. Положение в пространстве материальной точки полностью определяется заданием значений трех ее координат. Координаты могут быть декартовы (задаются проекции на координатные оси радиус-вектора точки x, y, z), цилиндрические (задаются две линейные координаты и одна угловая), сферические (задаются две угловые координаты и одна линейная) и т. д. В любом случае положение точки в пространстве полностью определяется тремя независимыми числами. В соответствии с этим материальная точка имеет три степени свободы.

Значит, на каждую степень свободы одноатомной молекулы приходится энергия, равная kT/2.

В классической (не квантовой) статистической физике доказывается следующая теорема (Больцман): если система молекул находится в тепловом равновесии при температуре Т, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна kT/2.

Эта теорема называется законом равномерного распределения кинетической энергии по степеням свободы, или, коротко, законом равнораспределения.

В отношении своей внутренней энергии двух- и многоатомные газы отличаются от одноатомных числом степеней свободы своих молекул. Значит, для вычисления внутренней энергии газа и, следовательно, теплоемкости надо уметь определять число степеней свободы молекул газа.

Рассмотрим сначала простейший случай – двухатомной молекулы. Ее можно себе представить в виде системы, состоящей из двух атомов, расположенных на некотором расстоянии друг от друга (рис. 34). Если расстояние между этими атомами не меняется (такие молекулы мы будем называть жесткими), то такая система вообще говоря, имеет шесть степеней свободы.

Действительно, положение и конфигурация такой молекулы определяются: тремя координатами ее центра масс, которыми определяется поступательное движение молекулы как целого, и тремя координатами, определяющими возможные вращения молекулы около взаимно перпендикулярных осей X, Y, Z.

Однако, если мы рассматриваем атомы идеального газа как материальные точки, то молекула не может вращаться вокруг оси X (см. рис. 34), на которой лежат центры обоих атомов. Поэтому для описания возможных вращений нашей молекулы достаточно двух координат.

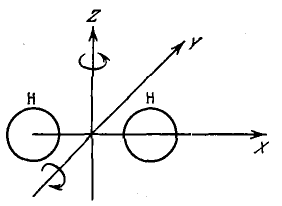
Рис. 34. Вращательные степени свободы 2-атомной молекулы

Следовательно, число степеней свободы жесткой двухатомной молекулы равно 5, из них три поступательные (как принято говорить) и две вращательные степени свободы.

Но атомы в молекуле не всегда жестко связаны друг с другом; они могут совершать колебания друг относительно друга. Тогда, очевидно, требуется еще одна координата для определения конфигурации молекулы, это — расстояние между атомами.

Следовательно, в общем случае двухатомная молекула обладает шестью степенями свободы: тремя поступательными, двумя вращательными и одной колебательной.

Если молекула состоит из п атомов, нежестко связанных, то она имеет 3n степеней свободы (каждый атом имеет три степени свободы). Из этого числа три степени свободы поступательные и три вращательные, за исключением случая, когда атомы расположены на одной прямой, — тогда вращательных степеней свободы только две (как у двухатомной молекулы).

Из опытов по измерению теплоемкости газов вытекает, что при определении числа степеней свободы молекулы атомы следует рассматривать как материальные точки. Следовательно, одноатомной молекуле нужно приписывать три поступательные степени свободы, двухатомной молекуле, в зависимости от характера связи между атомами, следует приписывать либо три поступательные и две вращательные степени свободы (при жесткой связи), либо, кроме этих пяти, еще одну, коле­бательную степень свободы (при упругой связи), трехатомной молекуле с жесткой связью — три поступательные и три вращательные степени свободы и т. д.

Согласно положению о равнораспределении среднее значение энергии одной молекулы i будет (при той же температуре) тем больше, чем сложнее молекула, чем больше у нее степеней свободы. При определении <ε> нужно учесть, что колебательная степень свободы должна обладать вдвое большей энергетической емкостью по сравнению с поступательной или вращательной.

Это объясняется тем, что поступательное и вращательное движение молекулы связано с наличием только кинетической энергии, в то время как колебательное движение связано с наличием и кинетической, и потенциальной энергии, причем для гармонического осциллятора среднее значение кинетической и потенциальной энергии оказывается одинаковым. Поэтому на каждую колебательную степень свободы должны приходиться в среднем две половинки kT — одна в виде кинетической энергии и одна в виде потенциальной.

Таким образом, средняя энергия молекулы должна равняться:

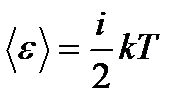, (90)

где i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы:

i = n_пост + n_вращ + 2n_колеб (91)

Для молекул с жесткой связью между атомами i совпадает с числом степеней свободы молекулы.

Таким образом, а внутренняя энергия одного моля газа определяется формулой:

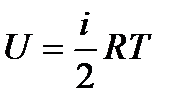. (92)

Соответственно этому молярные теплоемкости газа

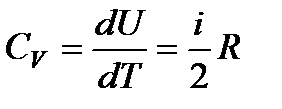, (93)

и

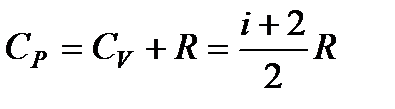. (94)