а) Если вероятность появления события в каждом независимом испытании постоянна и равна p, то вероятность появления события ровно k раз в серии из n испытаний вычисляется по формуле Бернулли
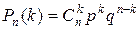 , где
, где 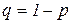 .
.
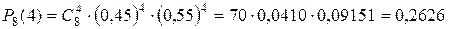 .
.
Заметим, что расчёты по формуле Бернулли при больших n достаточны сложны. Поэтому вероятность 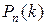 находится приближенно.
находится приближенно.
б) Если число независимых испытаний n велико (n > 100), а вероятность p появления события в каждом них мала (p £ 0,3), то для приближенного вычисления вероятности появления события ровно k раз в серии из n испытаний используется формула Пуассона
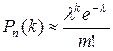 , где
, где 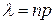 .
.
Условия пункта б) удовлетворяют вышеуказанным требованиям (n = 300 > 100, p = 0,02 < 0,3). Находим 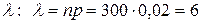 .
.
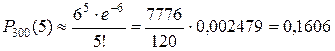 .
.
в) Если n достаточно большое и np ³ 7, то формула Пуассона даёт большую погрешность. В этом случае для вычисления используют локальную теорему Лапласа:
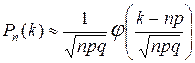 , где
, где 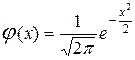 .
.
Функция 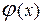 табулирована, её таблицы приведены в приложении учебника [4]. В таблицах помещены значения функции только для положительных значений аргумента х. Для отрицательных значений х использует те же таблицы, так как рассматриваемая функция – чётная.
табулирована, её таблицы приведены в приложении учебника [4]. В таблицах помещены значения функции только для положительных значений аргумента х. Для отрицательных значений х использует те же таблицы, так как рассматриваемая функция – чётная.
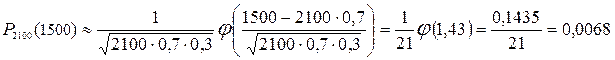 .
.
г) Если нас интересует вероятность, что событие появится не менее a раз и не более b раз при большом n, применяют формулу, которая выражает содержание интегральной теоремы Лапласа:
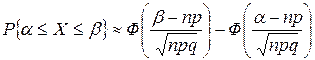 , где F(х)
, где F(х) 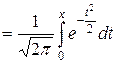
F(x) – функция Лапласа – также табулирована [4]. Уже при x = 5 функция F(x) очень мало отличается от 0,5 (F(5) = 0,499997). Поэтому для всех x > 5 принимается, что F(x)» 0,5. Функция Лапласа – нечётная функция, т.е. F(– x) = – F(x).
В нашем случае
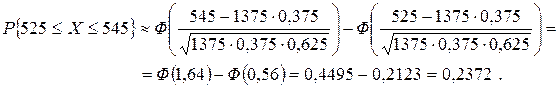
 2015-02-15
2015-02-15 2467
2467
