Физический смысл частотных характеристик цифровых и непрерывных систем очень близок. Особенностью этих характеристик для цифровых систем является то, что они устанавливают связь между гармоническими последовательностями (гармоническими решетчатыми функциями) на входе и выходе цифрового звена (системы) с дискретной передаточной функцией W( z ). Огибающие решетчатых функций изменяются по гармоническому закону.
по окончании переходного процесса

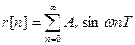
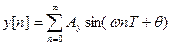
В отличие от непрерывной гармонической функции гармоническая решетчатая функция в общем случае не является периодической функцией n. Кроме того, амплитуды Аr и Ау не обязательно являются теми максимальными значениями, которых могут достигать те или иные члены соответствующих последовательностей r[n], y[n]. Амплитуды всегда будут определять лишь верхние границы, но не обязательно максимумы членов этих последовательностей.
Для перехода к частотным характеристикам используется замена аргумента
Z= e jωT,
в результате которой получаем комплексный передаточный коэффициент цифровой системы
W*(jω)=W( e jωT).
Пусть дискретная передаточная функция имеет вид
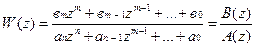 ,
,
тогда 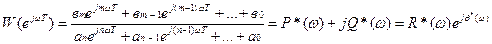 ,
,
где 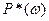 ,
, 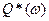 ,
, 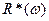 ,
, 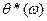 - соответственно вещественная, мнимая, амплитудная и фазовая частотные характеристики цифровой системы.
- соответственно вещественная, мнимая, амплитудная и фазовая частотные характеристики цифровой системы.
Очевидно,
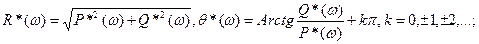
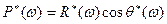 ,
, 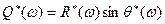 .
.
При фиксированном значении 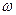 комплексный передаточный коэффициент изображается геометрически вектором на плоскости (P*,jQ*). При изменении
комплексный передаточный коэффициент изображается геометрически вектором на плоскости (P*,jQ*). При изменении 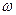 конец вектора W*(jω) прочерчивает некоторую кривую, которую называют годографом комплексного передаточного коэффициента системы или ее амплитудно-фазовой характеристикой.
конец вектора W*(jω) прочерчивает некоторую кривую, которую называют годографом комплексного передаточного коэффициента системы или ее амплитудно-фазовой характеристикой.
Основные особенности частотных характеристик цифровых систем, которые вытекают из свойств дискретной передаточной функции:
1. Частотные характеристики цифровых систем являются периодическими функ-циями относительно частоты 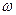 с периодом повторения ω0=2
с периодом повторения ω0=2 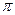 /T. Это означает, что при построении этих характеристик достаточно ограничиться изменением
/T. Это означает, что при построении этих характеристик достаточно ограничиться изменением 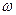 в диапазоне шириной 2
в диапазоне шириной 2 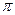 /Т, например от -
/Т, например от - 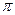 /Т до
/Т до 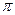 /Т. Если же учесть, что участки частотной характеристики в диапазонах ω от –
/Т. Если же учесть, что участки частотной характеристики в диапазонах ω от – 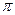 /Т до 0 и от 0 до
/Т до 0 и от 0 до 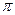 /Т симметричны (поскольку W*(jω) и W*(-jω) – комплексные сопряженные функции), то можно ограничиться построением частотной характеристики в интервале изменения
/Т симметричны (поскольку W*(jω) и W*(-jω) – комплексные сопряженные функции), то можно ограничиться построением частотной характеристики в интервале изменения 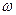 от 0 до
от 0 до 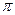 /Т;
/Т;
2. Амплитудно-фазовые частотные характеристики цифровой системы заканчиваются на вещественной оси, так как для 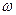 =
= 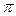 /Т комплексный передаточный коэффициент всегда является действительным числом.
/Т комплексный передаточный коэффициент всегда является действительным числом.
Свойство периодичности частотных характеристик цифровых систем физически объясняется стробоскопическим эффектом, который проявляется в том, что гармоническая решетчатая функция r[n] на входе дискретного звена не изменяется при изменении частоты ω огибающей на любую величину, кратную ω0, т.е. последовательность r[n] будет одной и той же при всех частотах огибающей, равных ω+kω0, k=0,1,2,3,… (рис. 1).
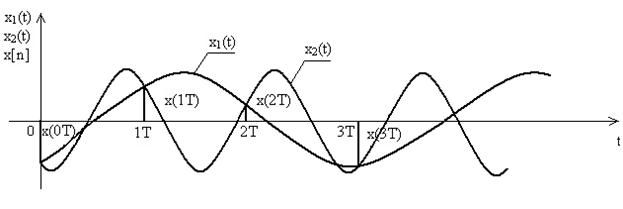
Рис. 1. Гармонические сигналы различных частот, соответствующие одной и той же решетчатой функции
ПРИМЕР:
Дискретная передаточная функция разомкнутой системы имеет вид
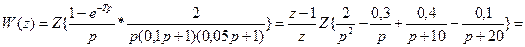
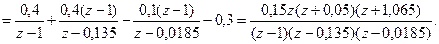
| |||
| |||
|
|
|

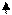
|
|
|
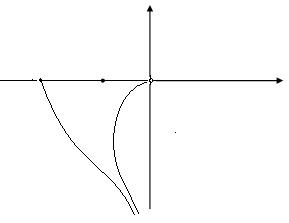
Рис. 2. Годографы W(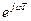 ), ω
), ω 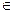 (0,
(0, 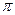 /Т)
/Т)
 2015-02-04
2015-02-04 1273
1273
