Угол между плоскостями
Пусть заданы две плоскости 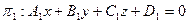
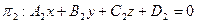 .
.
Углом между плоскостями называется один из двухгранных углов, образованных при пересечении этих плоскостей. Выпишем нормали к плоскостям: 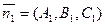 и
и 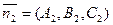 . Угол между плоскостями равен углу между нормалями к плоскостям, т.е.
. Угол между плоскостями равен углу между нормалями к плоскостям, т.е. 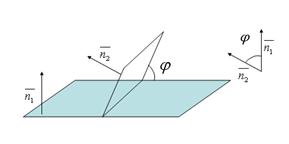 Косинус угла между плоскостями вычисляется по формуле:
Косинус угла между плоскостями вычисляется по формуле:
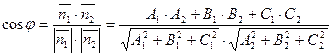 |
Условие перпендикулярности плоскостей:
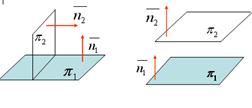
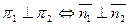 , это условие в векторной форме:
, это условие в векторной форме: 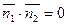 , или в координатной форме:
, или в координатной форме: 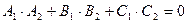
Условие параллельности плоскостей:
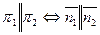 , или в координатной форме: координаты векторов должны быть пропорциональны:
, или в координатной форме: координаты векторов должны быть пропорциональны: 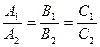
Расстояние от точки до плоскости
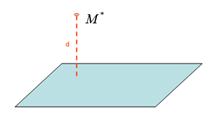 Пусть задана точка:
Пусть задана точка: 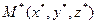 и плоскость:
и плоскость: 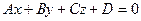 расстояние d от точки до плоскости находится по формуле:
расстояние d от точки до плоскости находится по формуле: 
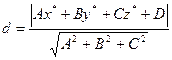 |
 2015-02-18
2015-02-18 1489
1489








