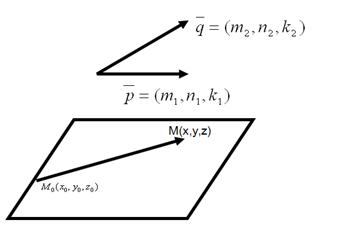
 Опр.: Два неколлинеарных вектора, параллельные плоскости, называются направляющими векторами этой плоскости.
Опр.: Два неколлинеарных вектора, параллельные плоскости, называются направляющими векторами этой плоскости.
Пусть необходимо составить уравнение плоскости, проходящей через заданную точку 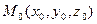 и параллельную заданным векторам
и параллельную заданным векторам 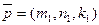 и
и 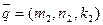 . Считаем, что такая плоскость построена, возьмем произвольную точку М (x,y,z) этой плоскости и составим вектор
. Считаем, что такая плоскость построена, возьмем произвольную точку М (x,y,z) этой плоскости и составим вектор 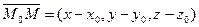 . При любом расположении точки М, векторы
. При любом расположении точки М, векторы 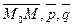 компланарны, т.е. их смешанное произведение равно 0. Запишем это условие в векторной форме:
компланарны, т.е. их смешанное произведение равно 0. Запишем это условие в векторной форме: 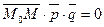 . Запишем в координатной форме:
. Запишем в координатной форме:
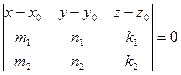 |
Данный способ задания плоскости называется плоскость по точке 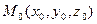 и двум направляющим векторам
и двум направляющим векторам 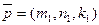 и
и 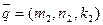 .
.
 2015-02-18
2015-02-18 20886
20886








