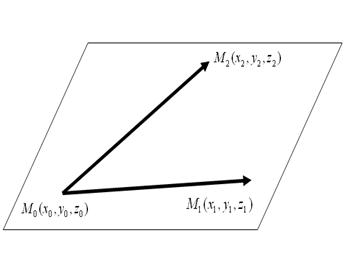
 Пусть необходимо составить уравнение плоскости, проходящей через три заданные, не лежащие на одной прямой, точки:
Пусть необходимо составить уравнение плоскости, проходящей через три заданные, не лежащие на одной прямой, точки: 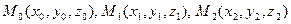
Считаем, что такая плоскость построена, составим два вектора 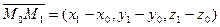 и
и 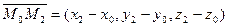 .
.
Эти векторы являются направляющими векторами плоскости. Составим уравнение плоскости по точке 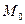 и двум направляющим векторам
и двум направляющим векторам 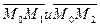 .
.
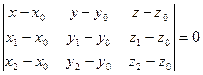 |
Данный способ задания плоскости называется плоскость по трем точкам.
Пример: Составить уравнение плоскости АВС, если даны координаты точек:
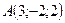 ;
; 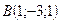 ;
; 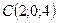
Решение: Составим уравнение плоскости 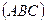 по трем точкам:
по трем точкам:
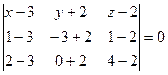 ,
, 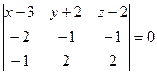 ,
,
Найдем разложение определителя по первой строке:
 ,
,
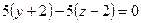 ,
,
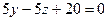 , разделим уравнение на 5:
, разделим уравнение на 5:
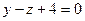 .
.
Ответ: 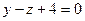 .
.
 2015-02-18
2015-02-18 7311
7311
