Разбиваем составное сечение на составляющие типовые сечения и определяем геометрические характеристики относительно их собственных центральных осей в соответствии с рисунком 2.5.
Для швеллера № 10 по ГОСТ 8240-89 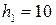 см,
см, 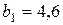 см,
см, 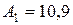 см 2,
см 2, 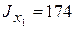 см 4,
см 4, 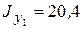 см 4,
см 4, 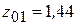 см,
см, 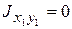 .
.
Для пластины 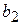 =20,0 см,
=20,0 см, 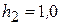 см,
см, 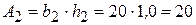 см 2,
см 2, 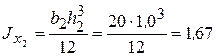 см 4;
см 4; 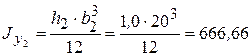 см 4;
см 4; 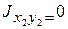
Для неравнобокого уголка № 7,5/5,0´0,5 по ГОСТ 8510-86 с учетом изменения положения осей 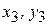 ;
; 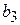 =7,5 см;
=7,5 см; 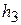 = 5,0 см;
= 5,0 см; 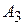 =6,11 см 2;
=6,11 см 2;
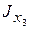 = 12,5 см 4;
= 12,5 см 4; 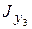 =34,8 см 4;
=34,8 см 4; 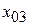 =2,39 см;
=2,39 см; 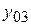 =1,17 см;
=1,17 см; 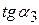 =0,436;
=0,436; 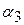 =23036¢
=23036¢
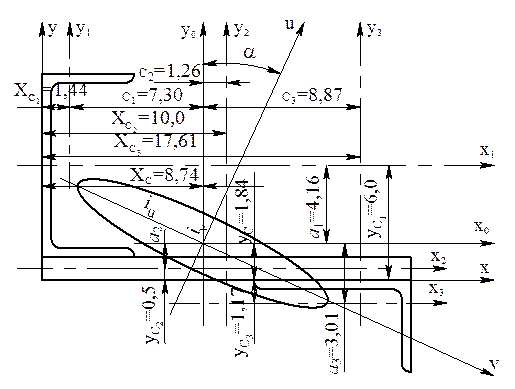
Рисунок 2.4

Рисунок 2.5
Центробежный момент инерции сечения неравнобокого уголка относительно собственных центральных осей определяется по формуле
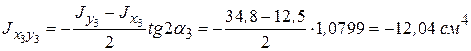
- где знак минус центробежного момента инерции определяется по его знакам в квадрантах относительно собственных центральных осей 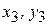 .
.
Ход решения
Вычерчиваем в масштабе составное сечение по заданному варианту задания и проводим вспомогательную систему координат x, y. Рисунок 2.4.
1. Определяем положение центра тяжести составного сечения относительно вспомогательной системы координат х, у.
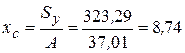 см;
см; 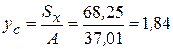 см
см
где 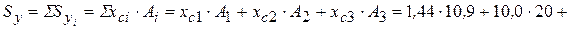
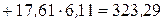 см 3 – статический момент площади составного сечения относительно вспомогательной оси у;
см 3 – статический момент площади составного сечения относительно вспомогательной оси у;
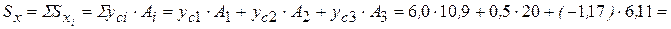
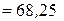 см 3 – статический момент площади составного сечения относительно вспомогательной оси х;
см 3 – статический момент площади составного сечения относительно вспомогательной оси х;
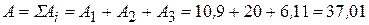 см 2 – площадь составного сечения;
см 2 – площадь составного сечения;
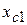 =1,44 см;
=1,44 см; 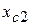 =10,0 см;
=10,0 см; 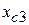 =17,61 см;
=17,61 см; 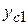 =6,0 см;
=6,0 см; 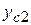 =0,5 см;
=0,5 см; 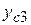 = -1,17 см – координаты центров тяжести типовых сечений относительно вспомогательных осей х, у.
= -1,17 см – координаты центров тяжести типовых сечений относительно вспомогательных осей х, у.
По найденным координатам строим положение центра тяжести составного сечения и проводим вспомогательные центральные оси х 0, у 0 параллельно вспомогательным осям х, у.
2. Определяем моменты инерции составного сечения относительно вспомогательных центральных осей х 0, у 0.
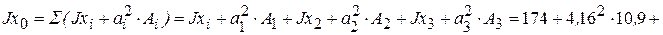
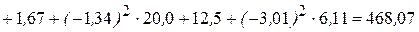 см 4
см 4
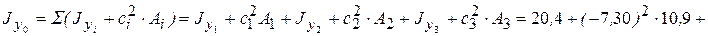
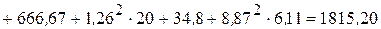 см 4
см 4



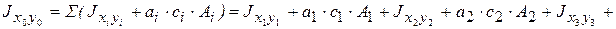

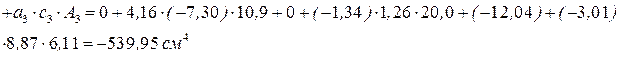
где 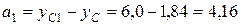 см,
см, 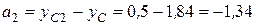 см,
см, 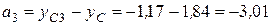 см,
см, 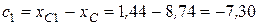 см,
см, 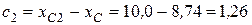 см,
см, 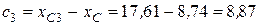 см,
см,
- расстояния между собственными центральными осями типовых сечений и вспомогательными центральными осями 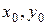 составного сечения.
составного сечения.
3. Определяем положение главных центральных осей
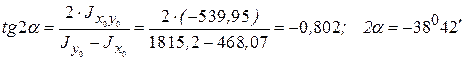 ;
; 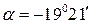
Строим положение главных центральных осей u, v откладывая угол a относительно осей 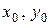 . Ось u откладывается от оси
. Ось u откладывается от оси 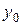 и ось v от оси
и ось v от оси 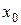 , т.к.
, т.к. 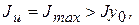 а
а 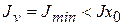 . Знак минус показывает, что угол
. Знак минус показывает, что угол 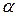 откладывается по часовой стрелке.
откладывается по часовой стрелке.
4. Определяем значение главных моментов инерции составного сечения
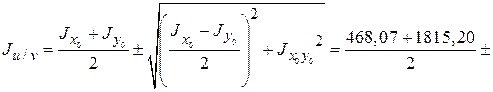
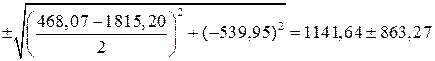
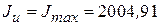 см4 ;
см4 ; 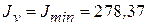 см 4
см 4
Проводим проверку правильности определения главных моментов инерции. Центробежный момент инерции относительно главных центральных осей 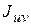 =0.
=0.
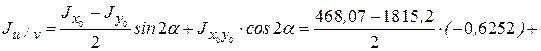
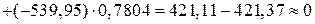
По закону постоянства суммы осевых моментов инерции
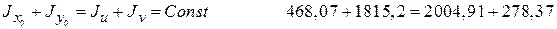 2283,27 см 4 = 2283,28 см 4
2283,27 см 4 = 2283,28 см 4
5. Определяем радиусы инерции эллипса инерции относительно главных осей u, v.
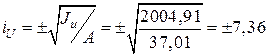 см,
см, 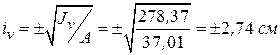
По найденным радиусам инерции строим эллипс инерции, откладывая их значения относительно соответствующих осей.
 2015-02-18
2015-02-18 2538
2538
