Пусть 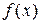 , определенная на отрезке
, определенная на отрезке 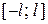 , имеет период
, имеет период 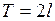 (
(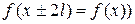 , где l –– произвольное положительное число) и удовлетворяет условиям Дирихле.
, где l –– произвольное положительное число) и удовлетворяет условиям Дирихле.
Разложение функции 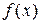 в ряд Фурье на отрезке
в ряд Фурье на отрезке 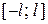 имеет вид
имеет вид
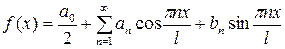 , (22)
, (22)
где 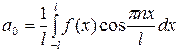 ,
, 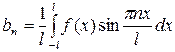
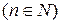 . (23)
. (23)
Ряд в правой части равенства (22) с коэффициентами, вычисляемыми по формулам (23), называется рядом Фурье для функции 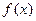 с периодом
с периодом 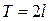 .
.
Замечание. Все теоремы, имеющие место для рядов Фурье 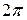 –– периодических функций, остаются в силе и для рядов Фурье функций, период которых
–– периодических функций, остаются в силе и для рядов Фурье функций, период которых 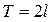 . В частности, если
. В частности, если 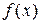 на отрезке
на отрезке 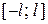 –– четная, то ее ряд Фурье имеет вид
–– четная, то ее ряд Фурье имеет вид
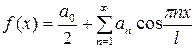 , (24)
, (24)
где 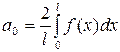 ,
, 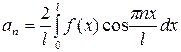
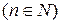 , (25)
, (25)
если 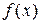 –– нечетная функция, то
–– нечетная функция, то
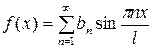 , (26)
, (26)
где 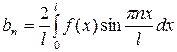 (
(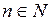 ). (27)
). (27)
Пример 32. Разложить функцию 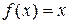 на интервале
на интервале 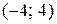 в ряд Фурье.
в ряд Фурье. 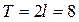 (рис. 5).
(рис. 5).
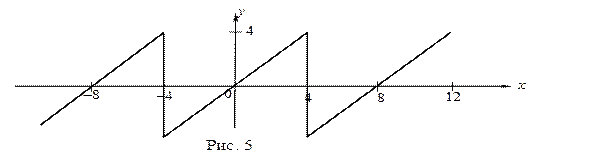
Решение. Данная функция –– нечетная, удовлетворяет условиям Дирихле.
По формулам (26) и (27) при 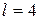 имеем
имеем 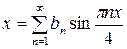 , где
, где 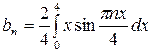
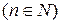 .
.
Вычислим
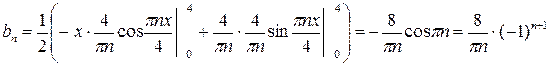
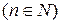 .
.
Таким образом, 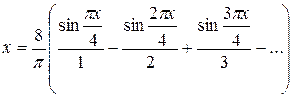 для
для 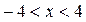 .
.
«Обыкновенные дифференциальные уравнения»
Ниже приведены примеры решения задач с некоторыми методическими указаниями.
Пример 1. Найти общее решение уравнения 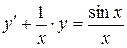 .
.
Это линейное уравнение первого порядка. Положим y = U · V, тогда y' = U' · V + U · V'.
Имеем 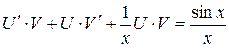 или
или 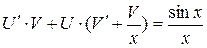 .
.
Пусть 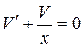 . Отсюда
. Отсюда 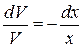 и, значит,
и, значит, 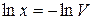 , т.е.
, т.е. 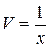 .
.
Следовательно, 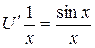 , откуда
, откуда 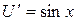 и, значит,
и, значит, 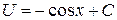 .
.
Имеем окончательно 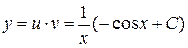 .
.
Пример 2. Найти общее решение уравнения 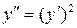 .
.
Положим 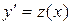 . Тогда
. Тогда 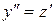 и уравнение имеет вид
и уравнение имеет вид 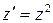 или
или 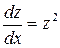 .
.
Проинтегрировав его, получим 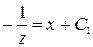 , или
, или 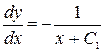 . Тогда
. Тогда 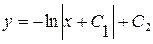 .
.
Пример 3. Найти общее решение уравнения 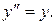
Положим 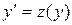 . Тогда
. Тогда 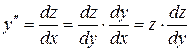 .
.
Уравнение теперь имеет вид 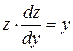 . Проинтегрировав его, получим
. Проинтегрировав его, получим 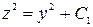 или
или 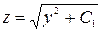 . Но
. Но 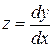 . Следовательно,
. Следовательно, 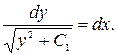
Интегрируя, получаем 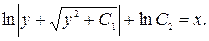 Общий интеграл дифференциального уравнения имеет вид
Общий интеграл дифференциального уравнения имеет вид 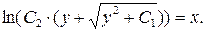
Пример 4. Найти общее решение линейного неоднородного дифференциального уравнения III порядка 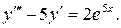
Составим характеристическое уравнение: 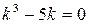 .
.
У него три действительных различных корня: 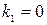 ,
, 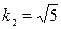 ,
, 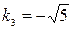 . Следовательно, общее решение соответствующего однородного уравнения имеет вид
. Следовательно, общее решение соответствующего однородного уравнения имеет вид 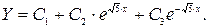 Правая часть неоднородного уравнения имеет форму
Правая часть неоднородного уравнения имеет форму 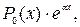 где
где 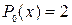 — многочлен нулевой степени, a = 5 не является корнем характеристического уравнения. Частное решение неоднородного уравнения будем искать в виде
— многочлен нулевой степени, a = 5 не является корнем характеристического уравнения. Частное решение неоднородного уравнения будем искать в виде 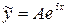 , где A — постоянная, которую нужно найти. Тогда
, где A — постоянная, которую нужно найти. Тогда 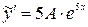 ,
, 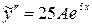 ,
, 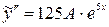 и получаем
и получаем 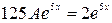 . Отсюда
. Отсюда 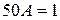 ,
, 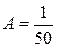 . Следовательно,
. Следовательно, 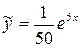 . Общим решением неоднородного уравнения будет
. Общим решением неоднородного уравнения будет 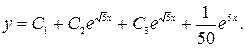
Пример 5. Найти вид общего решения уравнения 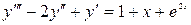 .
.
Характеристическое уравнение 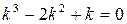 имеет корни:
имеет корни: 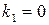 ,
, 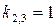 . Значит, общее решение соответствующего однородного уравнения будет равно
. Значит, общее решение соответствующего однородного уравнения будет равно 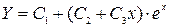 . Правая часть уравнения имеет форму
. Правая часть уравнения имеет форму 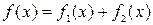 , где
, где
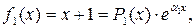 a 1 = 0,
a 1 = 0,
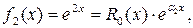 a 2 = 2.
a 2 = 2.
Частное решение  , соответствующее правой части
, соответствующее правой части 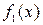 , ищем в виде
, ищем в виде 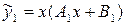 , а частное решение
, а частное решение 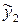 , соответствующее правой части
, соответствующее правой части 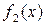 , — в виде
, — в виде 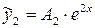 . Тогда общее решение неоднородного уравнения будет иметь вид
. Тогда общее решение неоднородного уравнения будет иметь вид 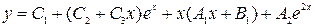 .
.
Пример 6. Найти вид общего решения уравнения 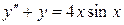 .
.
Характеристическое уравнение 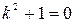 имеет корни
имеет корни 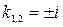 и, значит, общее решение соответствующего однородного уравнения будет
и, значит, общее решение соответствующего однородного уравнения будет 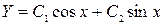 . Правая часть уравнения имеет форму
. Правая часть уравнения имеет форму 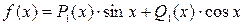 . Поэтому частное решение неоднородного уравнения будем записывать в виде
. Поэтому частное решение неоднородного уравнения будем записывать в виде
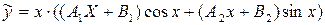 ,
,
так как пара ± i является корнями характеристического уравнения. Общее решение неоднородного уравнения будет иметь вид
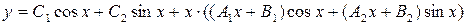 .
.
Пример 7. Найти решение уравнения 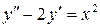 , удовлетворяющее условиям y (0) = 0, у ΄(0) = 0.
, удовлетворяющее условиям y (0) = 0, у ΄(0) = 0.
Характеристическое уравнение 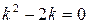 имеет два корня: k 1 = 0, k 2 = 2. Значит, общим решением соответствующего однородного уравнения будет
имеет два корня: k 1 = 0, k 2 = 2. Значит, общим решением соответствующего однородного уравнения будет 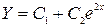 .
.
Так как правая часть уравнения имеет форму 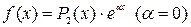 , то частное решение неоднородного уравнения выберем в виде
, то частное решение неоднородного уравнения выберем в виде 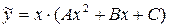 (так как a = 0 есть корень характеристического уравнения). Подставив
(так как a = 0 есть корень характеристического уравнения). Подставив 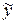 в уравнение, получим
в уравнение, получим
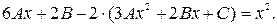
Отсюда –6 A = 1; 6 A – 4 B = 0; 2 B – 2 C = 0.
Следовательно, 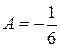 ,
, 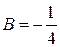 ,
, 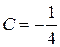 , а общее решение
, а общее решение 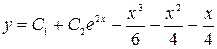 . Так как y (0) = C 1 + C 2 = 0, то C 1 = – C 2. Производная
. Так как y (0) = C 1 + C 2 = 0, то C 1 = – C 2. Производная
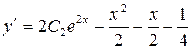 при x = 0 равна нулю, значит
при x = 0 равна нулю, значит 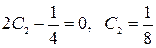 и
и 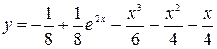 — искомое решение.
— искомое решение.
Пример 8. Найти общее решение уравнения 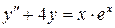 .
.
Характеристическое уравнение k 2 + 4 = 0 имеет корни k 1,2 = ±2 i. Значит, общее решение соответствующего однородного уравнения запишется в виде Y = C 1cos2 x + C 2sin2 x. Функция, стоящая в правой части дифференциального уравнения, имеет вид 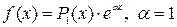 . Так как a = 1 не является корнем характеристического уравнения, то частным решением неоднородного уравнения будет
. Так как a = 1 не является корнем характеристического уравнения, то частным решением неоднородного уравнения будет 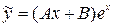 . Подставив в уравнение
. Подставив в уравнение 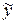 ,
, 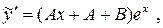
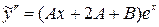 , получим
, получим 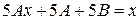 , т.е. 5 A = 1,
, т.е. 5 A = 1, 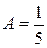 ,
, 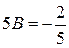 ,
, 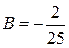 . Значит, частное решение неоднородного уравнения
. Значит, частное решение неоднородного уравнения 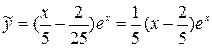 , а общее решение имеет вид
, а общее решение имеет вид
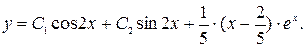
Пример 9. Найти общее решение уравнения 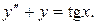
Однородному уравнению 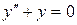 соответствует характеристическое уравнение k 2 + 1 = 0. Его корни k 1,2 = ± i. Поэтому y 1 = cos x и y 2 = sin x будут решениями однородного уравнения.
соответствует характеристическое уравнение k 2 + 1 = 0. Его корни k 1,2 = ± i. Поэтому y 1 = cos x и y 2 = sin x будут решениями однородного уравнения.
Запишем решение неоднородного уравнения в виде 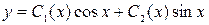 и составим систему уравнений для отыскания C 1 и C 2.
и составим систему уравнений для отыскания C 1 и C 2.
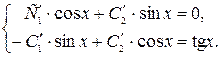
Решив ее, найдем 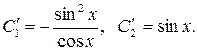
Интегрирование дает 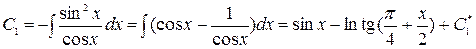 ,
,
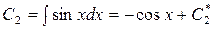 ,
,
где 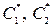 — произвольные постоянные.
— произвольные постоянные.
Общим решением уравнения будет
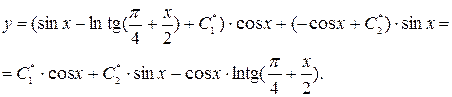
«мНОГОМЕРНЫЕ ИНТЕГРАЛЫ»
 2015-02-04
2015-02-04 4540
4540
