I способ. Предположим, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a, x = b и кривыми 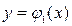 ,
, 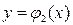 , причем функции
, причем функции 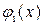 ,
, 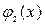 непрерывны и
непрерывны и 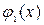
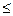
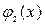 для всех
для всех 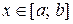 (рис. 1).
(рис. 1).
Такая область называется правильной в направлении оси Oy: любая прямая, параллельная оси Oy, пересекает границу области D не более чем в двух точках. В этом случае двойной интеграл сводится к двукратному по формуле
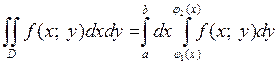 . (1)
. (1)
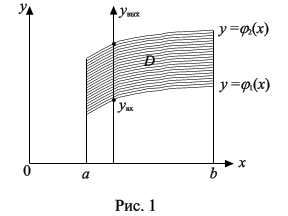
II способ. Если область D ограничена прямыми y = с и y = d (c < d), кривыми 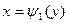 и
и 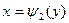 , причем
, причем 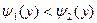 для всех
для всех 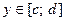 (рис. 2), т.е. область D –– правильная в направлении оси Ox, то
(рис. 2), т.е. область D –– правильная в направлении оси Ox, то
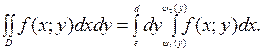 (2)
(2)
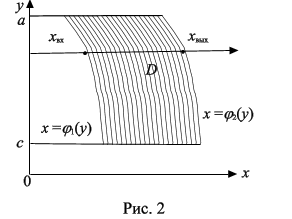
Пример 1. В интеграле 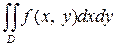 расставить пределы интегрирования двумя способами, если область ограничена линиями x = 1, y = x 2, y = 2 x (x
расставить пределы интегрирования двумя способами, если область ограничена линиями x = 1, y = x 2, y = 2 x (x 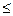 1).
1).
Решение. I способ. Изобразим область D (рис. 3а).
При каждом значении x 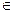 [0; 1] переменная y изменяется от x 2 до 2 x, т.е. область D можно представить в виде
[0; 1] переменная y изменяется от x 2 до 2 x, т.е. область D можно представить в виде 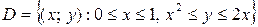 Тогда двойной интеграл можно представить в виде двукратного по формуле (1)
Тогда двойной интеграл можно представить в виде двукратного по формуле (1)
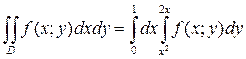 .
.
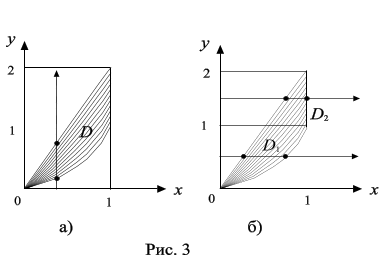
II способ. Чтобы воспользоваться формулой (2), нужно разбить область D на две части D 1 и D 2 так, как показано на рис. 3б. В области D 1 переменная y изменяется от 0 до 1, а при каждом значении y переменная x изменяется от y /2 (значение x на прямой y = 2 x) до 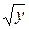 (значение x на параболе y = x 2). Поэтому по формуле (2) получаем
(значение x на параболе y = x 2). Поэтому по формуле (2) получаем
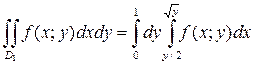 .
.
В области D 2 переменная y изменяется от 1 до 2, а при каждом значении y переменная x изменяется от y /2 до 1. По формуле (2) имеем
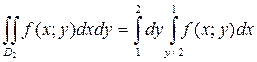 .
.
Итак,
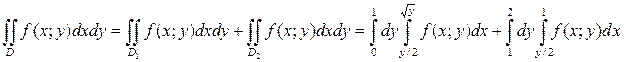 .
.
 2015-02-04
2015-02-04 1695
1695








