Теорема Дирихле. Пусть 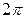 –– периодическая функция
–– периодическая функция 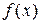 на отрезке
на отрезке 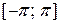
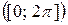 удовлетворяет двум условиям:
удовлетворяет двум условиям:
1) 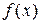 –– кусочно-непрерывная, т.е. непрерывная или имеет конечное число точек разрыва I рода;
–– кусочно-непрерывная, т.е. непрерывная или имеет конечное число точек разрыва I рода;
2) 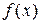 –– кусочно-монотонная, т.е. монотонная на всем отрезке либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонная.
–– кусочно-монотонная, т.е. монотонная на всем отрезке либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонная.
Тогда соответствующий функции 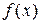 ряд Фурье сходится на этом отрезке и при этом:
ряд Фурье сходится на этом отрезке и при этом:
1) в точках непрерывности функции сумма ряда 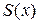 совпадает с самой функцией:
совпадает с самой функцией: 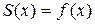 ;
;
2) в каждой точке 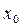 разрыва функции
разрыва функции
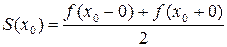 ,
,
т.е. сумма ряда равна среднему арифметическому пределов функции 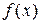 справа и слева;
справа и слева;
3) в точках 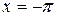 и
и 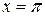 (или при
(или при 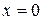 ,
, 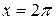 на концах отрезка)
на концах отрезка)
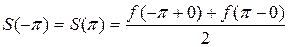 .
.
Таким образом, если функция 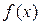 удовлетворяет условиям 1 и 2 теоремы Дирихле, то на отрезке
удовлетворяет условиям 1 и 2 теоремы Дирихле, то на отрезке 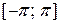
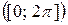 имеет место разложение (16):
имеет место разложение (16):
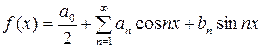 ,
,
причем коэффициенты вычисляются по формулам (17). Это равенство может нарушиться только в точках разрыва функции 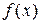 и на концах отрезка
и на концах отрезка 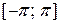 .
.
В силу периодичности исходной функции и суммы ряда Фурье может быть получено указанное разложение во всей области определения функции.
Пример 30. Разложить в ряд Фурье функцию 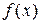 периода
периода 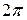 , заданную на отрезке
, заданную на отрезке 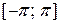 формулой
формулой 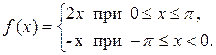
Решение. На рис. 1 изображен график функции 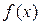 . Эта функция удовлетворяет условиям Дирихле, значит она может быть разложена в ряд Фурье. Находим коэффициенты ряда:
. Эта функция удовлетворяет условиям Дирихле, значит она может быть разложена в ряд Фурье. Находим коэффициенты ряда:
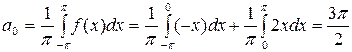 ;
;
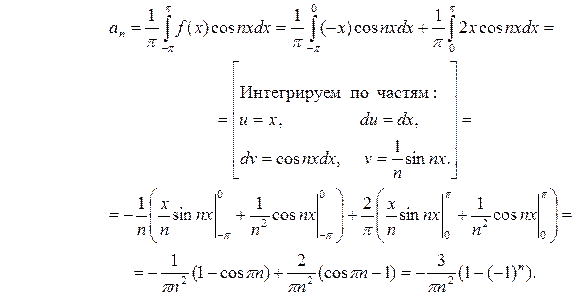
Аналогично находим
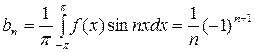 .
.
Исходной функции 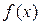 соответствует ряд Фурье
соответствует ряд Фурье
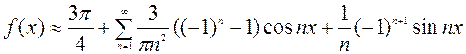 .
.
Функция 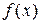 непрерывна во всех внутренних точках отрезка
непрерывна во всех внутренних точках отрезка 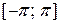 , поэтому, согласно теореме Дирихле, для всех этих точек имеем равенство
, поэтому, согласно теореме Дирихле, для всех этих точек имеем равенство 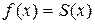 , т.е.
, т.е.
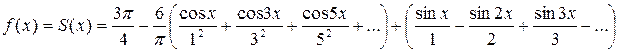 .
.
В точках 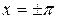 сумма ряда
сумма ряда 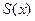 равна
равна
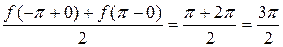 .
.
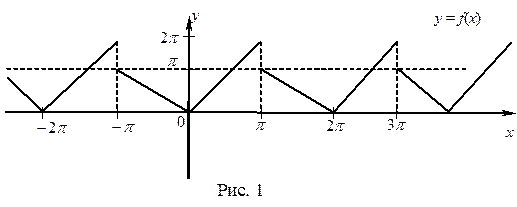
График функции 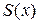 показан на рис. 2.
показан на рис. 2.
 2015-02-04
2015-02-04 6612
6612
