Разложение в ряд Фурье четных и нечетных функций

Если функция 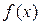— четная, то ее ряд Фурье имеет вид

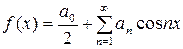, (18)

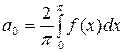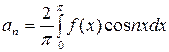
где , 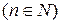. (19)

Если функция 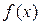— нечетная, то ее ряд Фурье имеет вид

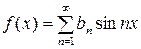, (20)

где 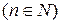. (21)

Ряды (18) и (20) называются неполными тригонометрическими рядами или рядами по косинусам и по синусам соответственно.

Пример 31. Разложить в неполный тригонометрический ряд по косинусам функцию 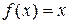при 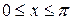, 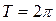. Построить график суммы .

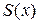Решение. Продолжим данную функцию четным образом в интервал: 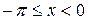и построим ее периодическое продолжение (рис. 3).

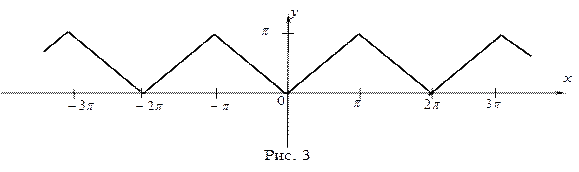
Функция будет иметь вид 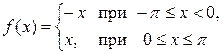и удовлетворять условиям Дирихле. Так как 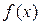–– четная, то 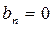. Вычислим 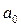и 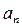по формулам (19):

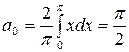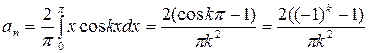, для .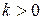

Отсюда получаем, что заданная функция 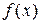на интервале 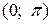представляется рядом .

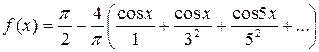При этом .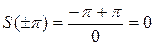

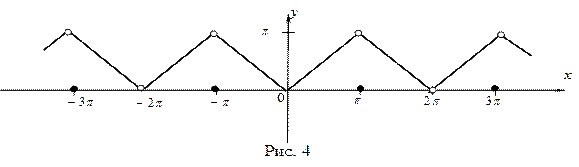
График 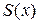имеет вид, показанный на рис. 4.