Разложение функций в ряд Фурье

С помощью так называемого тригонометрического ряда любую (практически) периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники.

Тригонометрическим рядом называется функциональный ряд вида

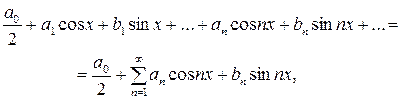(15)

где действительные числа 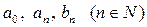называются коэффициентами ряда.

Пусть 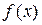–– произвольная периодическая функция с периодом 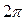. Предположим, что функция 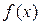разлагается в тригонометрический ряд, т.е. 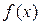является суммой ряда (15):

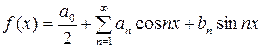. (16)

Коэффициенты 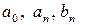вычисляются по формулам:

; ;

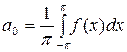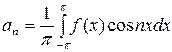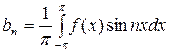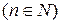, . (17)

Числа 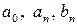, определяемые по формулам (17), называются коэффициентами Фурье функции 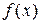, а тригонометрический ряд (15) с такими коэффициентами –– рядом Фурье функции .

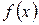Для того, чтобы 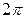–– периодическую функцию 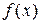можно было представить в виде ряда Фурье, который бы сходился к свой сумме S (x), требуется выполнение дополнительных условий.