1. Масса плоской фигуры. Если для плоской пластинки D известна переменная плотность 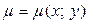 , то ее масса находится по формуле
, то ее масса находится по формуле 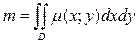 .
.
2. Статические моменты и координаты центра тяжести плоской фигуры.
Статические моменты фигуры D относительно осей Ox и Oy могут быть вычислены по формулам:
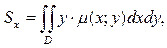
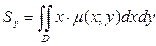 .
.
Координаты центра масс фигуры определяются по формулам:
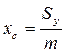 ,
, 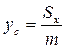 .
.
3. Моменты инерции плоской фигуры. Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d от точки до оси, т.е. Ml = m ∙ d 2. Моменты инерции плоской фигуры относительно осей Ox и Oy могут быть вычислены по формулам:
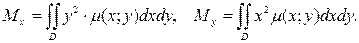
Момент инерции фигуры относительно начала координат –– по формуле M 0 = Mx + My.
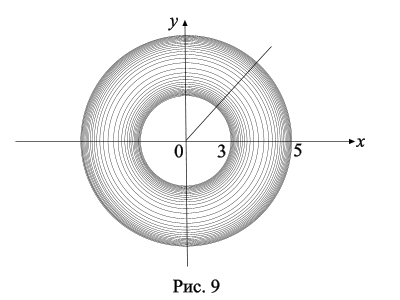
Пример 5. Вычислить массу пластинки, имеющей форму кольца, образованного концентрическими окружностями с радиусами 3 и 5, если плотность пластинки обратно пропорциональна расстоянию от центра этих окружностей.
Решение. Поместим начало координат в центр пластинки (рис. 9).
Масса плоской пластинки вычисляется по формуле: 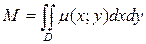 , где
, где
D –– область пластинки, а 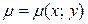 –– плотность пластинки в точке (x; y). По условию
–– плотность пластинки в точке (x; y). По условию 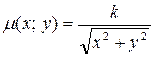 , где k –– постоянный коэффициент пропорциональности. Отсюда
, где k –– постоянный коэффициент пропорциональности. Отсюда
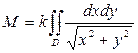 .
.
Переходя к полярным координатам, получаем
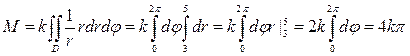 (ед. массы).
(ед. массы).
 2015-02-04
2015-02-04 2212
2212








