Объем тела V находится по формулам: 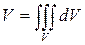 или
или
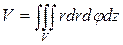 – в цилиндрических;
– в цилиндрических;
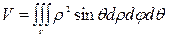 – в сферических.
– в сферических.
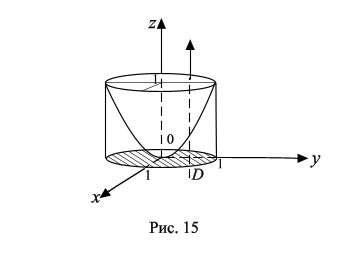
Пример 8.1. Найти объем тела, ограниченного поверхностями: z = x 2 + y 2 и z = 1. Сделать чертеж.
Решение. Данное тело ограничено сверху плоскостью z = 1, снизу – параболоидом z = x 2 + y 2 (рис. 15). Объем тела находим, используя цилиндрические координаты:
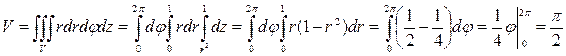 (куб. ед.).
(куб. ед.).
Пример 8.2. Найти объем тела, ограниченного поверхностями:
z = 4 x 2+ 2 y 2+ 1, x + y – 3 = 0, x = 0, y = 0, z = 0. Сделать чертеж.
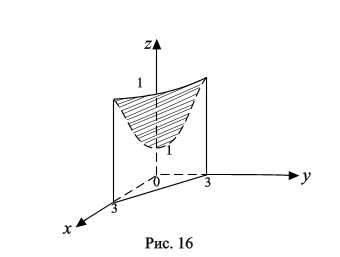
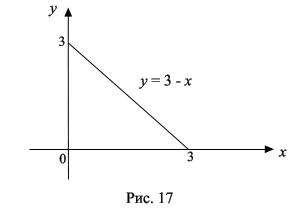
Решение. Данное тело ограничено сверху частью параболоида z = 4 x 2 + 2 y 2 + 1, снизу –– плоскостью z = 0, боковые поверхности: x = 0, y = 0 x + y = 3 (рис. 16). Проекцией тела на плоскость xOy есть треугольник (рис. 17).
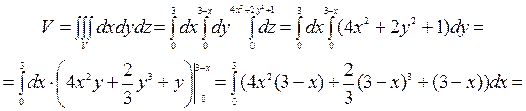
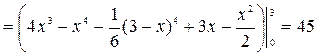 (куб. ед.).
(куб. ед.).
 2015-02-04
2015-02-04 25468
25468
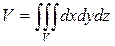 – в
– в 






