Если область интегрирования образована цилиндрической поверхностью, то при вычислении тройного интеграла бывает удобно перейти к цилиндрическим координатам. При этом
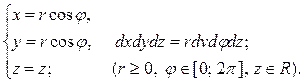
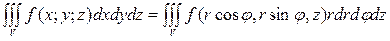 . (6)
. (6)
Если же область интегрирования есть шар или часть его, то вычисления лучше вести в сферических координатах:
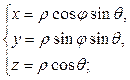
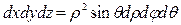 ;
;
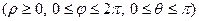 ;
;
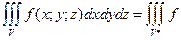
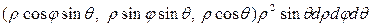 . (7)
. (7)
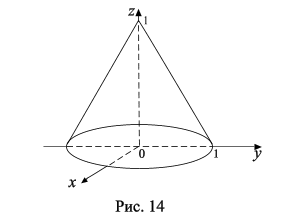
Пример 7.1. Вычислить 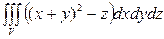 , если область V ограничена поверхностями z = 0 и (z – 1)2 = x 2 + y 2.
, если область V ограничена поверхностями z = 0 и (z – 1)2 = x 2 + y 2.
Решение. 1. Область V представляет собой конус, при этом 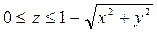 . Проекция этого конуса на плоскость xOy есть круг с центром в точке (0; 0) и R = 1.
. Проекция этого конуса на плоскость xOy есть круг с центром в точке (0; 0) и R = 1.
2. Для вычисления интеграла удобней перейти к цилиндрическим координатам:
a) 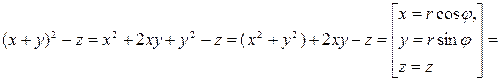
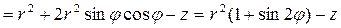 ;
;
б) 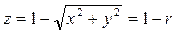 ;
;
в) 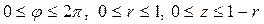 ;
;
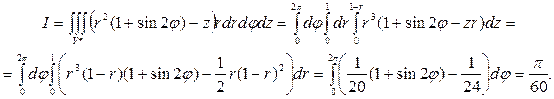
Пример 7.2. Вычислить 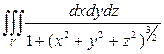 , где V –– шар: x 2 + y 2 + z 2
, где V –– шар: x 2 + y 2 + z 2 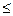 1.
1.
Решение. Вычислим интеграл с помощью сферических координат: x = r cos 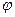 sin
sin 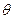 , y = r sin
, y = r sin 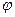 sin
sin 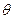 , z = r cos
, z = r cos 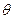 . Тогда dxdydz = r 2sin
. Тогда dxdydz = r 2sin 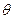 d
d 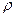 d
d 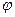 d
d 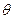 .
.
Граница области V –– сфера и ее уравнение имеет вид
x 2 + y 2 + z 2 = 1; r 2cos2 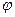 sin2
sin2 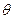 + r 2sin2
+ r 2sin2 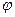 sin2
sin2 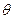 + r 2cos2
+ r 2cos2 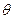 =
=
= r 2sin2 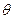 (cos2
(cos2 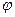 + sin2
+ sin2 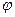 ) + r 2cos2
) + r 2cos2 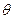 = r 2sin2
= r 2sin2 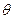 + r 2cos2
+ r 2cos2 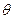 = r 2 = 1, т.е. r = 1.
= r 2 = 1, т.е. r = 1.
Подынтегральная функция после замены переменных примет вид
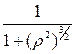 , т.е.
, т.е. 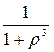 .
.
Новые переменные изменяются в следующих пределах:
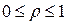 ,
, 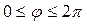 ,
, 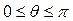 .
.
Таким образом, согласно формуле (7)
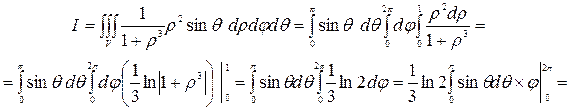
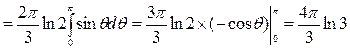 .
.
 2015-02-04
2015-02-04 2309
2309








