Точечные оценки параметров не дают информации о степени близости к соответствующему теоретическому параметру. Если объем выборки мал, то точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. Вычисленная точечная оценка может быть близка к оцениваемому параметру, а может и очень сильно отличаться от него. Точечная оценка не несет информацию о точности процедуры оценивания.
Интервальная оценка – это числовой интервал, который определяется двумя числами – границами интервала - и содержащий неизвестный параметр генеральной совокупности.
Пусть имеется выборка объема 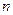 и
и 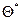 - статистическая оценка неизвестного параметра
- статистическая оценка неизвестного параметра 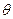 (
(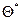 - случайная величина, т.к. найдена по выборочным данным).
- случайная величина, т.к. найдена по выборочным данным).
Доверительным интервалом называется интервал со случайными границами (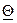 ,
, 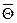 ), в котором с заданной вероятностью
), в котором с заданной вероятностью  находится оцениваемый параметр
находится оцениваемый параметр 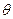
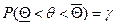
Вероятность  называется доверительной вероятностью.
называется доверительной вероятностью.
Доверительная вероятность задается априорно. Чем ближе  к единице, тем точнее оценка. Для практических целей обычно выбирают
к единице, тем точнее оценка. Для практических целей обычно выбирают 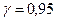 ; 0,99 или 0,9973. Доверительная вероятность, например, 0,95 означает, что мы пренебрегаем возможностью появления события (считаем его невозможным), вероятность которого меньше 1-0,95=0,05.
; 0,99 или 0,9973. Доверительная вероятность, например, 0,95 означает, что мы пренебрегаем возможностью появления события (считаем его невозможным), вероятность которого меньше 1-0,95=0,05.
Т.к. при различных выборках получаются различные значения оценки 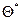 , то и доверительные границы изменяются от выборки к выборке. Поэтому лучше говорить не о вероятности попадания параметра в доверительный интервал, а о вероятности того, что доверительный интервал накроет параметр
, то и доверительные границы изменяются от выборки к выборке. Поэтому лучше говорить не о вероятности попадания параметра в доверительный интервал, а о вероятности того, что доверительный интервал накроет параметр 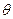 .
.
Доверительный интервал применяется в случае сравнительно небольшого объема выборки, когда предполагается, что надежность точечной оценки может быть невысокой.
Доверительный интервал для оценки математического ожидания случайной величины 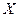 с заданной надежностью
с заданной надежностью 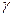 в случае нормального закона распределения определяется на основе неравенств
в случае нормального закона распределения определяется на основе неравенств
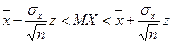 ,
,
где 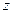 — значение аргумента функции Лапласа, получаемое из таблиц (см. Приложение 1), с учетом того, что
— значение аргумента функции Лапласа, получаемое из таблиц (см. Приложение 1), с учетом того, что  ;
;
 — известное среднее квадратичное отклонение или его оценка;
— известное среднее квадратичное отклонение или его оценка;
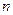 — объем выборки.
— объем выборки.
Пример 1. Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания нормально распределенной случайной величины 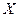 , если известны ее среднее квадратическое отклонение
, если известны ее среднее квадратическое отклонение 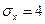 , выборочное среднее
, выборочное среднее 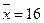 и объем выборки
и объем выборки 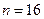 .
.
Решение. По надежности 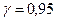 из соотношения
из соотношения  находим значение функции Лапласа:
находим значение функции Лапласа: 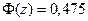 .
.
По таблице значений функции Лапласа (см. Приложение 1) находим 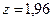 . Используя неравенства для интервальной оценки математического ожидания, получаем
. Используя неравенства для интервальной оценки математического ожидания, получаем
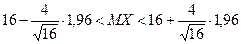
или 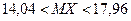 .
.
 2015-02-24
2015-02-24 888
888








