2015-02-24
1375
1. Найти доверительный интервал с надежностью 0,8 для оценки математического ожидания нормально распределенной случайной величины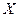 
со средне квадратическим отклонением 
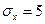, выборочным средним 
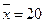и объемом выборки 
.
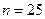2. На овцеводческой ферме из стада произведена выборка для взвешивания 36 овец. Их средний вес оказался равным 50 кг. Предположив распределение веса нормальным и определив несмещенную оценку выборочной дисперсии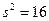 
, найти доверительный интервал для оценки математического ожидания с надежностью а) 0,8; б) 0,9; в) 0,95.
3. Из генеральной совокупности извлечена выборка объемом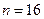 
и найдено выборочное среднее, равное 30. Получено также несмещенное значение выборочной дисперсии 
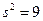. Предположив распределение случайной величины 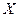нормальным, найти доверительный интервал для оценки математического ожидания с надежностью а) 0,8 и б) 0,9.
4. Случайная величина 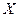распределена по нормальному закону. Статистическое распределение выборки представлено в таблице
 | |||||||
 |
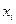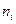Найти с надежностью 0,97 доверительный интервал для оценки математического ожидания.
5. Случайная величина 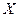распределена по нормальному закону. Статистическое распределение выборки представлено в таблице:
| | |||||
| |
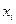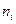Найти с надежностью 0,95 доверительный интервал для оценки математического ожидания.
