Дифференциальное уравнение первого порядка называется линейным, если оно линейно относительно неизвестной функции и её производной, т. е. содержит у и у ′ в первой степени.
Линейное уравнение можно привести к виду
y' + p(x)y = q (х) (9)
где р (х) и q (х) – заданные непрерывные функции от х (или постоянные).
В частности, уравнение y' + p(x)y =0называется линейным без правой части или линейным однородным.
В линейном однородном уравнении 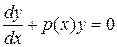 переменные разделяются:
переменные разделяются:
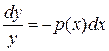
и поэтому его интегрирование сводится к вычислению интегралов от обеих частей равенства:
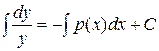 .
.
Для того чтобы решить уравнение (9) при q (х) ≠ 0, будем искать неизвестную функцию у в виде произведения двух пока неизвестных функций от х, т. е. положим у = и (х) v (х). Тогда у' = и' (х) v (х) + и (х) v' (х). Подставив значения у и y ′ в уравнение (9):
и' v + иv' + иv p(x) = q (х),
после группировки получим
v [ и' + иp(x) ]+ иv' = q (х) (9′)
Так как у есть произведение двух функций то одна из них может быть выбрана произвольно, другая же должна определяться уравнением (9′).
Выберем и (х) так, чтобы выражение, стоящее в квадратных скобках, обращалось в нуль, т. е. и' + иp(x) = 0. Это уравнение с разделяющимися переменными:

откуда
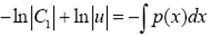
или
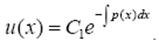
Для большей простоты выкладок берем частное решение 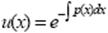 , отвечающее значению С 1 = 0. Подставив найденное значение и (х) в уравнение (9′), получим (учитывая, что
, отвечающее значению С 1 = 0. Подставив найденное значение и (х) в уравнение (9′), получим (учитывая, что
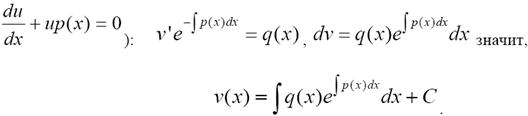
Подставив и (х) и v (х) в формулу у = и (х) v (х), найдем общее решение уравнения (9). Уравнение (9) может быть решено методом вариации произвольной постоянной, который будет рассмотрен ниже.
Пример. Решить дифференциальное уравнение y' + 2 xy = 2 x 2 e - x 2.
Решение. Положим у = иv, тогда y' = u'v + v'u; подставим у и у ′ в данное уравнение:
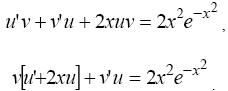 . (*)
. (*)
Так как одну из вспомогательных функций и или v можно взять произвольно, то выберем в качестве и какой-либо частный интеграл уравнения 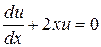 или
или 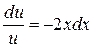 . Проинтегрировав, получим ln| u | = − x 2 (С = 0), откуда u = e - x 2 . Подставив это выражение в уравнение (*), получим
. Проинтегрировав, получим ln| u | = − x 2 (С = 0), откуда u = e - x 2 . Подставив это выражение в уравнение (*), получим
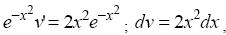
отсюда находим
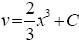
и, следовательно, общим решением будет 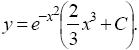
1.5. Уравнение Бернулли
Уравнением Бернулли называется дифференциальное уравнение первого порядка вида
y' + p(x)y = q (х) у m, (10)
где m ¹0 и m ¹ 1 (в противном случае получилось бы линейное уравнение). Как и линейное, уравнение Бернулли можно проинтегрировать с помощью подстановки у = и (х) v (x) или свести к линейному уравнению с помощью подстановки z = y 1 -m . Разделив обе части уравнения на уm, получим
y -m y' + p(x) y 1 -m = q (х) (10 ')
Сделаем далее замену: z = y 1 -m . Тогда
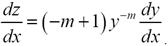
Подставив z и dz / dx в уравнение (10′), будем иметь линейное уравнение
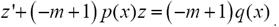
Решая это уравнение и переходя от z снова к у, получим решение исходного уравнения.
Пример. Решить уравнение. 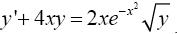
Решение. Разделив все члены уравнения на 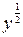 , получим
, получим
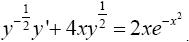 (*)
(*)
Введем новую функцию y = 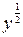 , тогда
, тогда
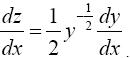
Подставив эти значения в уравнение (*), получим линейное уравнение
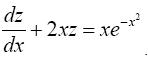 (**)
(**)
Найдем его общий интеграл:
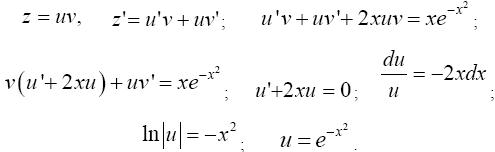
Для определения v получим уравнение 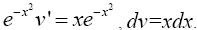
Интегрируя, найдем
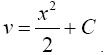
Следовательно, решением уравнения (**) будет функция 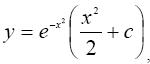 а исходного −
а исходного − 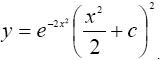
 2015-03-22
2015-03-22 761
761








