Мы убедились, что, в случае когда известно общее решение линейного однородного уравнения, можно по методу вариации произвольных постоянных найти общее решение неоднородного уравнения. Однако вопрос о том, как найти общее решение однородного уравнения, остался открытым. В частном случае, когда в линейном дифференциальном уравнении (3) все коэффициенты рi (х) = аi − константы, он решается достаточно просто, даже без интегрирования.
Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами, т. е. уравнения вида
y (n) + а 1 y (n – 1) +… аn – 1 y' + аny = 0, (14)
где аi − константы (i = 1, 2,..., n).
Как известно, для линейного однородного уравнения 1-го порядка решением является функция вида е kx. Будем искать решение уравнения (14) в виде j (х) = е kx.
Подставим в уравнение (14) функцию j (х) и ее производные порядка m (1 ≤ m ≤ n) j (m)(х) = kmе kx. Получим
(kn + а 1 kn – 1 +… аn – 1 k + аn) е kx = 0,
но е kх ≠ 0 при любом х, поэтому
kn + а 1 kn – 1 +… аn – 1 k + аn = 0. (15)
Уравнение (15) называется характеристическим уравнением, многочлен, стоящий в левой части, − характеристическим многочленом, его корни − характеристическими корнями дифференциального уравнения (14).
Вывод: функция j (х) = е kx − решение линейного однородного уравнения (14) тогда и только тогда, когда число k − корень характеристического уравнения (15).
Таким образом, процесс решения линейного однородного уравнения (14) сводится к решению алгебраического уравнения (15).
Возможны различные случаи характеристических корней.
1. Все корни характеристического уравнения действительные и различные.
В этом случае n различным характеристическим корням k 1, k 2, ..., kn соответствует n различныx решений однородного уравнения (14)
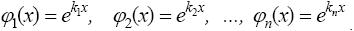
Можно показать, что эти решения линейно независимы, следовательно, образуют фундаментальную систему решений. Таким образом, общим решением уравнения является функция
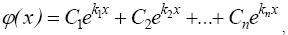
где С 1, C 2 ,..., Сn − произвольные константы.
Пример 7. Найти общее решение линейного однородного уравнения:
а) у ′′(х) − 6 у ′(х) + 8 у (х) = 0,
б) у ′′′(х) + 2 у ′′(х) − 3 у ′(х) = 0.
Решение. Составим характеристическое уравнение. Для этого заменим производную порядка m функции y (x) на соответствующую степень
k (у (m)(x) ↔ km),
при этом сама функция у (х) как производная нулевого порядка заменяется на k 0 = 1.
В случае (а) характеристическое уравнение имеет вид k 2− 6 k + 8 = 0. Корни этого квадратного уравнения k 1 = 2, k 2 = 4. Так как они действительные и различные, то общее решение имеет вид j (х) = С 1 е 2 х + С2 е 4 х .
Для случая (б) характеристическим уравнением является уравнение 3-й степени k 3 + 2 k 2 − 3 k = 0. Найдем корни этого уравнения:
k (k 2 + 2 k − 3) = 0 ⇒ k = 0 и k 2 + 2 k − 3 = 0 ⇒ k = 0, (k − 1)(k + 3) = 0,
т. е. k 1 = 0, k 2 = 1, k 3 = −3.
Этим характеристическим корням соответствует фундаментальная система решений дифференциального уравнения:
j1(х) = е 0 х = 1, j2(х) = е х, j3(х) = е −3 х .
Общим решением, согласно формуле (9), является функция
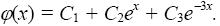
II. Все корни характеристического уравнения различные, но среди них есть комплексные.
Все коэффициенты дифференциального уравнения (14), а следовательно, и его характеристического уравнения (15) − действительные числа, значит, если cреди характеристических корней есть комплексный корень k 1 = а + ib, то есть и сопряженный ему корень k 2 = а − ib. Первому корню k 1 соответствует решение дифференциального уравнения (14)
j1(х) = е (a + ib) х = еaхеibх = еaх (cosbx + isinbx)
(воспользовались формулой Эйлера еiх = cosx + isinx). Аналогично, корню k 2 = а − ib соответствует решение
j2(х) = е (a - ib) х = е aхе − ibх = еaх (cosbx − isinbx).
Данные решения являются комплексными. Чтобы получить из них действиительные решения, воспользуемся свойствами решений линейного однородного уравнения. Функции
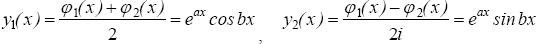
являются действительными решениями уравнения (14). Кроме того, эти решения линейно независимы 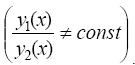 Таким образом, можно сделать следующий вывод.
Таким образом, можно сделать следующий вывод.
Правило 1. Паре сопряженных комплексных корней а ± ib характеристического уравнения в ФСР линейного однородного уравнения (14) соответствует два действительных частных решения
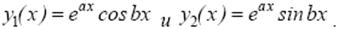
П р и м е р 8. Найти общее решение уравнения:
а) у ′′(х) − 2 у ′(х) + 5 у (х) = 0;
б) у ′′′(х) − у ′′(х) + 4 у ′(х) − 4 у (х) = 0.
Решение. В случае уравнения (а) корнями характеристического уравнения k 2 − 2 k + 5 = 0 являются два сопряженных комплексных числа
k 1, 2 = 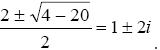
Следовательно, им, согласно правилу 1, соответствует два действительных линейно независимых решения: 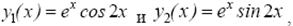 а общим решением уравнения является функция
а общим решением уравнения является функция
j (х) = С 1 ехcos 2 x + С 2 ехsin 2 x.
В случае (б), чтобы найти корни характеристического уравнения k 3 − k 2 + 4 k − 4 = 0, разложим на множители его левую часть:
k 2(k − 1) + 4(k − 1) = 0 ⇒ (k − 1)(k 2 + 4) = 0 ⇒ (k − 1) = 0, (k 2 + 4) = 0.
Следовательно, имеем три характеристических корня: k 1 = 1, k 2, 3 = ± 2 i. Корню k 1 соответствует решение 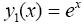 , а паре сопряженных комплексных корней k 2, 3 = ± 2 i = 0 ± 2 i − два действительных решения:
, а паре сопряженных комплексных корней k 2, 3 = ± 2 i = 0 ± 2 i − два действительных решения:
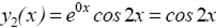 и
и 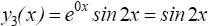 .
.
Составляем общее решение уравнения:
j (х) = С 1 ех + С 2 cos 2 x + С 3 sin 2 x.
III. Cреди корней характеристического уравнения есть кратные.
Пусть k 1 − действительный корень кратности m характеристического уравнения (15), т. е. среди корней есть m равных корней. Каждому из них соответствует одно и то же решение дифференциального уравнения (14) 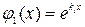 . Однако включить m равных решений в ФСР нельзя, так как они составляют линейно зависимую систему функций. Можно показать, что в случае кратного корня k 1решениями уравнения (14), кроме функции
. Однако включить m равных решений в ФСР нельзя, так как они составляют линейно зависимую систему функций. Можно показать, что в случае кратного корня k 1решениями уравнения (14), кроме функции 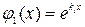 являются функции
являются функции
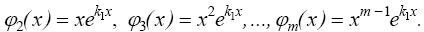
Функции j 1(х), j 2(х), …, jm (х) линейно независимы на всей числовой оси, т.к.
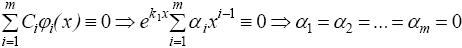 ,
,
т. е. их можно включить в ФСР.
Правило 2. Действительному характеристическому корню k 1 кратности m в ФСР соответствует m решений:
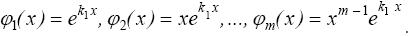
Если k 1 − комплексный корень кратности m характеристического уравнения (15), то существует сопряженный ему корень 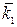 кратности m. По аналогии получаем следующее правило.
кратности m. По аналогии получаем следующее правило.
Правило 3. Паре сопряженных комплексных корней a ± ib в ФСР соответствует 2m действительных линейно независимых решений:
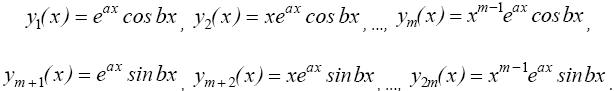
П р и м е р 9. Найти общее решение уравнения:
а) у ′′′(х) + 3 у ′′(х) + 3 у ′(х) + у (х)= 0;
б) уIV (х) + 6 у ′′ (х) + 9 у (х) = 0.
Решение. В случае (а) характеристическое уравнение имеет вид
k 3 + 3 k 2 + 3 k + 1 = 0
или
(k + 1)3 = 0,
т. е. k = −1 − корень кратности 3. На основании правила 2 записываем общее решение:
j(х) = С 1 + С 2 e − x + С 3 x 2 e − x.
Характеристическим уравнением в случае (б) является уравнение
k 4 + 6 k 2 + 9 = 0
или, иначе,
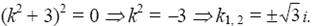
Имеем пару сопряженных комплексных корней, каждый из которых кратности 2. Согласно правилу 3 общее решение записывается в виде
j (х) = С 1 cos 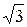 x+ С 2 xcos
x+ С 2 xcos 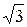 x+ С 3 sin
x+ С 3 sin 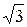 x+ С 4 xsin
x+ С 4 xsin 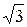 x.
x.
Из сказанного выше следует, что для любого линейного однородного уравнения с постоянными коэффициентами можно найти фундаментальную систему решений и составить общее решение. Следовательно, решение соответствующего неоднородного уравнения при любой непрерывной функции f (x) в правой части можно найти, используя метод вариации произвольных постоянных.
Пример 10. Методом вариации найти общее решение неоднородного уравнения у ′′(х) − у ′(х) − 6 у (х) = x e 2 x .
Решение. Сначала найдем общее решение соответствующего однородного уравнения у ′′(х) − у ′(х) − 6 у (х) = 0. Корнями характеристического уравнения k 2 − k − 6 = 0 являются k 1 = 3, k 2 = −2, а общим решением однородного уравнения − функция 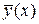 = С 1 е 3 х + С 2 е −2 х .
= С 1 е 3 х + С 2 е −2 х .
Будем искать решение неоднородного уравнения в виде
у (х) = С 1(х) е 3 х + С 2(х) е −2 х . (*)
Найдем определитель Вронского
W [ е 3 х , е −2 х ] = 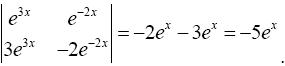
Составим систему уравнений (12) относительно производных неизвестных функций С ′1(х) и С ′2(х):
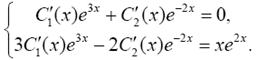
Решая систему по формулам Крамера, получим
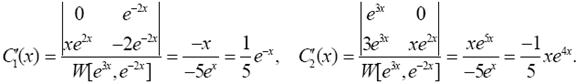
Интегрируя, найдем С 1(х) и С 2(х):
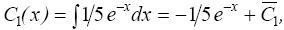
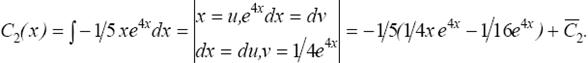
Подставляя функции С 1(х) и С 2(х) в равенство (*), получим общее решение уравнения у ′′(х) − у ′(х) − 6 у (х) = x e 2 x :
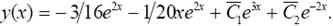
 2015-03-22
2015-03-22 10008
10008
