Определение определенного интеграла

Рассмотрим криволинейную трапецию аАВb (рис. 1), т. е. фигу­ру, ограниченную сверху графиком непрерывной функции y = f (x), (f (x) ≥ 0), слева и справа − отрезками аА и bВ прямых х = а, х = в, снизу − осью Оx. Разобьем отрезок точками

a = x ₀ < x ₁ < x ₂ < …<x_{i −1} < x_i < … < x_{n −1} < x_n = b

на n элементарных отрезков [ х_{i −1}, х_i ] (i = 1, 2, …, n), длины которых обозначим через Δ xi = x_i – x_{i- 1}. Прямыми x = xi (i = 1, 2, …, n) криволинейную трапецию aABb разобьем на n элементарных трапеций. В каждом из элементарных отрез­ков [ x_{i −1}, x_i ] выберем произвольную точку ξ _i ∈[ x_{i −1}, x_i ] и вычислим f( ξ _i ). Произведение f( ξ _i ) Δ x_i выражает площадь прямоугольника с основанием Δ x_i и высотой f( ξ _i ), и эта площадь приближенно равна площади Δ S_i i -й элемен­тарной трапеции Δ Si ≈ f( ξ _i i) Δ xi, а площадь S всей трапеции aABb равна приближенно

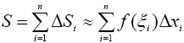
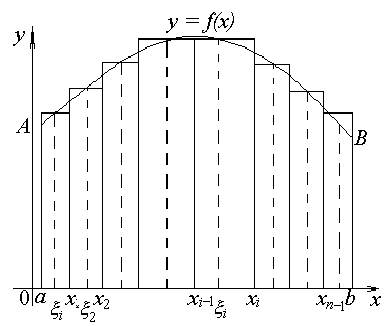
Сумму

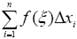
называют интегральной для функции f(x) на отрезке [ a, b ]. Очевидно, интег­раль­ная сумма для функции f(x) и отрезка [ a, b ] зависит от способа разбиения отрезка [ a, b ] и выбора точек ξ_i, т. е.

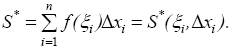
Рис. 1

Предел интегральной суммы (при условии, что длина наибольшего отрезка Δ x_i стремится к нулю) примем за площадь SaABb криволинейной трапеции:

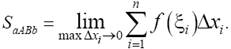
Определение 1. Пусть на отрезке [ a, b ] задана функция f(x). Отрезок [ a, b ] точками a = x ₀ < x ₁ < x ₂ < …< x_{n − 1} < b = x_n разобьем на n элементарных отрезков [ x_{i −1}, x_i ] (i = 1, 2, …, n) длины Δ x_i = x_i − x_{i −1}, в каждом из этих отрезков [ x_{i −1}, x_i ] возьмем произвольную точку ξ_i и составим сумму

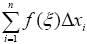
называемую интегральной суммой для функции f(x) на отрезке [ a, b ]. Если существует конечный предел последовательности интегральных сумм, при условии, что длина наибольшего Δ x_i из элементарных отрезков стремится к нулю (n → ∞), и предел не зависит ни от способа разбиения отрезка [ a, b ], ни от выбора точек ξi, то этот предел называется определенным интегралом от функции f(x) на отрезке [ a, b ] и обозначается

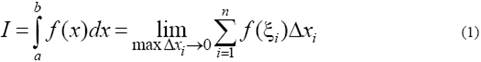
Здесь f(x) называется подынтегральной функцией, x − переменной интегри­рования, a и b − нижним и верхним пределами интегрирования.

Поэтому можно сформулировать понятие определенного интеграла так: число I называется определенным интегралом от функции f(x) на отрезке [ a, b ], если для любого ξ > 0существует δ > 0такое, что при max Δ x_i < δ (т. е. отрезок [ a, b ] разбит на части Δ x_i < δ) независимо от выбора точек ξ _i и способа разбиения выполняется неравенство

.

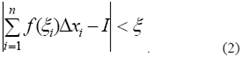Из всего сказанного следует, что если f(x) > 0на отрезке [ a, b ], то площадь S криволинейной трапеции aABb (рис. 1)

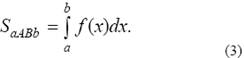
Функция, для которой существует предел (1) называется интегрируе­мой на отрезке [ a, b ].

Очевидно, если функция f (x) интегрируема на отрезке [ a, b ], то она ограничена на этом отрезке. В самом деле, если f (x) не ограничена на отрезке [ a, b ], то она не ограничена на некотором элементарном отрезке [ x_{i −1}, x_i ]. За счет выбора точки ξ _i интегральную сумму можно сделать сколько угодно большой, а такая интегральная сумма не имеет конечного предела.

Можно показать, что обратное утверждение не верно: существуют огра­ни­ченные функции, не являющиеся интегрируемыми.

Сформулируем без доказательства следующие утверждения:

1. Если функция f (x) непрерывна на отрезке [ a, b ], то она и интегрируема на этом отрезке.

2. Если функция f (x) имеет на отрезке [ a, b ] конечное число точек разры­ва первого рода, то она интегрируема на [ a, b ].