Экономико-математическая постановка задач массового обслуживания

Правильная экономико-математическая постановка задачи в значительной степени определяет эффективность рекомендаций по совершенствованию массового обслуживания в торговле, в сфере услуг и т.д. В связи с этим необходимо наблюдать за обслуживанием, выявлять сущест­венные связи проблемы, формировать цели и определять экономи­ческие критерии оценки работы СМО. В качестве общего, интег­рального критерия могут выступать затраты, с одной стороны, СМО как обслуживающей системы, а с другой — заявок, кото­рые могут иметь разную базу. Например, для товаров, поступающих в торго­вую сеть, этот критерий связан со временем и скоростью их обраще­ния и интенсивностью поступления денежных средств в банк.

Рассмотрим моделирование СМО в торговле. Оно должно включать анализ затрат времени в процессе обслуживания, например продавцов или населения в актах продажи-покупки товаров. Затем с помощью соответствующих методов и приемов необходимо строить модели свя­зи с другими показателями СМО торговли.

Например, особенностью показателей для СМО с отказами яв­ляется то, что время ожидания заявок в очереди Т_оч = 0. Поскольку в этом случае существование очереди невозможно, то l_оч = 0 и, следовательно, вероятность ее образования р_оч = 0. По числу заявок k определяются режим работы системы, ее состояние: при k = 0 — простой каналов, при 1<k<n — обслуживание заявок, при k>n — обслуживание и отказ. Показателями таких СМО являются: вероятность отказа в обслуживании р_отк, вероятность обслуживания р_обс, среднее время простоя канала T_пp, среднее число соответственно занятых и свободных каналов N_з и N_св, среднее вре­мя обслуживания Т_обс, абсолютная пропускная способность А.

Для СМО с неограниченным ожиданием характерно, что веро­ятность обслуживания заявки р_обс = 1, поскольку длина очереди и время ожидания начала обслуживания не ограничены, т. е. фор­мально 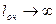и 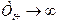. В таких системах возможны следующие режимы работы: при k = 0 наблюдается простой каналов обслужи­вания, при 1<k<n — обслуживание и при k>n — обслуживание и очередь. Показателями эффективности таких СМО являются: среднее число заявок в очереди l_оч, среднее число заявок в системе N_сист, среднее время пребывания заявки в системе T_сис, абсолютная про­пускная способность А.

В СМО с ожиданием с ограничением на длину очереди mах l_оч = m; если число заявок в системе k = 0, то наблюдается простой каналов. При 1<k<n — обслуживание, при n<k<n+m — обслуживание и очередь и при k > n+m — обслуживание, очередь и отказ в обслуживании. Показателями эффективности таких СМО являются вероятность отказа в обслуживании р_отк, вероятность обслуживания р_обс, среднее число заявок в очереди l_оч, среднее число заявок в системе N_сист, среднее время пребывания заявки в си­стеме T_сис, абсолютная пропускная способность А.

В процессе постановки задачи необходимо раскрыть взаимо­связи показателей эффективности СМО, которые по своей базовой принадлежности можно разделить на две группы, которые образуют две совокупности.

Первая группа показателей связана с издержками обращения торговли С_ио, которые определяются числом занятых обслужива­нием каналов, затратами на содержание СМО, интенсивностью обслуживания, степенью загрузки каналов, эффективностью их использования, пропускной способностью СМО и т.п.

Вторая группа показателей определяется издержками соб­ственно заявок С_из, поступающих на обслуживание, которые обра­зуют входящий поток и связаны с такими показателями, как длина очереди, время ожидания обслуживания, вероятность отказа в об­служивании, время пребывания заявки в СМО и др.

Обобщенным показателем эффективности СМО, включающим требования и возможности обеих групп, может быть крите­рий экономической эффективности, включающий как издержки обращения С_ио, так и издержки заявок С_из, которые будут иметь оптимальное значение при минимуме общих затрат С. На этом основании целевую функцию задачи можно записать так: С = (С_ио + С_из) → min.

Поскольку издержки обращения включают затраты, связанные с эксплуатацией СМО (С_экс) и простоем каналов обслуживания (С_пр), а издержки заявок включают потери, связанные с уходом необслуженных заявок (С_нз) и с пребыванием в очереди (С_оч), то целевую функцию можно переписать с учетом общих показателей таким образом:

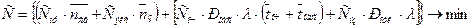. (5.9)

В зависимости от поставленной задачи управляемыми показателями могут быть: количество каналов обслуживания, организация кана­лов обслуживания (параллельно, последовательно, смешанным образом), дисциплина очереди, приоритет в обслуживании заявок, взаимопомощь между каналами и др. Часть показателей в задаче фигурирует в качестве неуправляемых, они обычно являются исход­ными данными. Следует заметить, что в качестве критерия эффек­тивности в целевой функции может быть товарооборот торгового предприятия или, например, рентабельность. Тогда, очевидно, оптимальные значения управляемых показателей СМО находятся уже при их максимальном значении и необходимо соответствующим образом провести преобразования целевой функции.

После построения целевой функции необходимо определить условия решения задачи, т. е. найти ограничения, установить ис­ходные значения показателей, выделить неуправляемые показатели и построить или подобрать совокупность моделей взаимосвязи всех показателей для анализируемого типа СМО, чтобы в конечном итоге найти оптимальные значения управляемых показателей, на­пример, количество продавцов, кассиров, грузчиков, фасовщиков, объемы складских помещений, размещение товаров в торговом зале и др.

Лекция 6. Методы и модели сетевого планирования и управления

Учебные вопросы

1 Особенности и назначение систем сетевого планирования и управления.

2 Основные понятия, определения и графические обозначения СПУ.

3 Правила построения сетевых графиков.

4 Основные параметры сетевых моделей и методы их расчета.

5 Постановка задач для решения методами СПУ.

6 Виды и сущность оптимизации сетевых моделей.

1 Особенности и назначение систем сетевого планирования и управления

Разнообразие и взаимозависимость задач, решаемых в области планирования и управления деятельностью коллективов или ряда организаций, располагающих материальными, финансовыми и другими ресурсами и имеющими общую задачу обеспечить достижение определенной цели, требуют научно обосно­ванной системы планирования и контроля за ходом выполнения работ. Для этой цели используют такой эффективный инструмент, как сетевые методы и модели, на базе которых создаются системы сетевого планирова­ния и управления (СПУ).

СПУ предназначены для управления сложными объектами, получившими название комплексов взаимосвязанных работ, операций, тем, разработок, требующих четкой координации действий множества исполнителей, а также для выполнения большого объема работ с высокой вероятностью соблюдения заданных сроков.

В СПУ применяется графическое изображение или аналитическая запись плана работ, в которой отражаются их логическая последовательность, взаимосвязь и продолжительность, т.е. используется информационно-динамическая модель особого вида (сетевая модель). Они выполняются с целью оптимизации разработанного плана и текущего управления ходом работ путем периодического сбора информации и соответствующей корректировки плана.

Перечислим основные преимущества систем СПУ, заключающиеся в том, что применение этих систем позволяет:

а) четко отобразить объем и структуру всего комп­лекса работ, выполнение которых необходимо для соз­дания объекта, и установить рациональную степень де­тализации работ для различных уровней управления;

б) выявить и всесторонне проанализировать все за­висимости между работами и иметь наглядное изобра­жение их технологической последовательности;

в) составить обоснованный план выполнения комп­лекса работ по созданию объекта;

г) осуществить обоснованное прогнозирование кри­тических работ и сконцентрировать внимание руководства на их первоочередном выполнении;

д) анализировать различные варианты плана по расчётным данным сетевой модели с выяснением влия­ния отдельных факторов на выбор наиболее эффектив­ного пути для достижения поставленной цели. Вносить в результате анализа изменения, направленные на улуч­шение плана (изменение сроков, технологической после­довательности, перераспределение ресурсов и т.д.);

е) получать на любой период необходимые расчет­ные данные в связи с возникающими расхождениями между намеченным планом и фактическим выполнением, а также использовать эти данные для выбора оптималь­ных решений по методам и средствам осуществления работ, подлежащих выполнению в последующие периоды;

ж) эффективно использовать и при необходимости перераспределять ресурсы в ходе осуществления плана, направляя их прежде всего на выполнение критических работ;

з) использовать для обработки больших массивов информации современные средства вычислительной тех­ники и благодаря этому быстро получать аналитические и отчетные данные, а также осуществлять непрерывное планирование работ путем корректировки планов с уче­том возникающих изменений.

Например, в торговле методы и модели СПУ могут применяться при выпол­нении следующих работ: заготовке, переработке и закладке пло­доовощной продукции на длительное хранение; переводе магазина на самообслуживание; строительстве универсальной оптовой базы, разработке плана развития торговой сети; планировании торговой деятельности; составлении бухгалтерского отчета; разработке торгово-финансового плана; поставке товаров покупателям; заключе­нии договоров на поставку; открытии нового торгового предприя­тия; проведении текущего или капитального ремонта; реконструк­ции торговых предприятий; подготовке и проведении оптовых ярмарок; организации и проведении выставок-продаж товаров и др.