Операции над пределами

1. Предел постоянной есть сама постоянная: 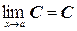, где С = const.

Следующие свойства справедливы при предположении, что функции f (x) и g (x) имеют конечные пределы при х ® а;

2. Предел суммы (разности) равен сумме (разности) пределов:

;

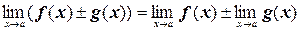3. Предел произведения равен произведению пределов:

;

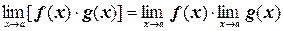4. Постоянную можно выносить за знак предела:

;

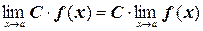5. Предел отношения равен отношению пределов:

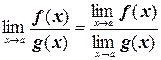, при ;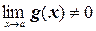

6. Если f (x)> 0 вблизи точки х = а и 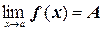, то А >0.

Аналогично определяется знак предела при f (x) < 0, f (x) ³ 0, f (x) £ 0;

7. Если g (x) £ f (x) £ u (x) вблизи точки х = а и 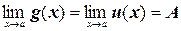, то и ;

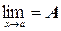8. ;

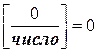9. ;

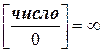10. ;

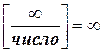11. ;

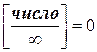12. Неопределенность вида 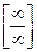можно раскрыть, если числитель и знаменатель дроби разделить на высшую степень переменной;

13. Неопределенность вида 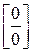можно раскрыть, если числитель и знаменатель дроби разложить на множители и сократить.