Примеры. №1. Используя свойства пределов функций, найти следующие пределы

№1. Используя свойства пределов функций, найти следующие пределы:

а)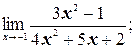

б)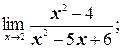

в)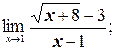

г)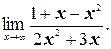

Решение.

а) Применяя теорему о действиях над пределами функций, получим:

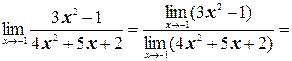
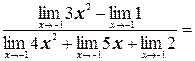
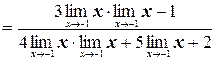
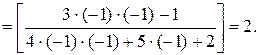
б) Так как пределы числителя и знаменателя при х ®2 равны нулю, то мы имеем неопределенность вида 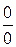. «Раскроем» эту неопределенность (т.е. избавимся от нее), разложив числитель и знаменатель на множители и сократив их далее на общий множитель х– 2:

.

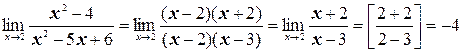в) Здесь мы также имеем неопределенность вида 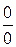. Домножим числитель и знаменатель дроби на выражение, сопряженное к числителю (избавимся от иррациональности в числителе):

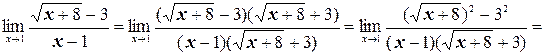
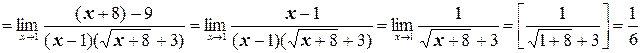
г) Числитель и знаменатель дроби – бесконечно большие функции, поэтому здесь имеет место неопределенность вида 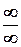. Раскроем эту неопределенность. Поделим числитель и знаменатель дроби на высшую степень х, т.е. на х ²:

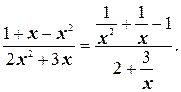
Таким образом,

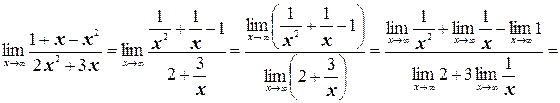
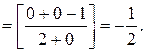
№2. Найти пределы:

а)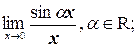

б)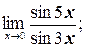

в)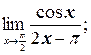

г)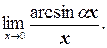

Решение.

а) Сделаем замену у=αх; тогда у ®0 при х ®0 и 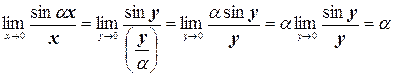. В последнем равенстве мы воспользовались первым замечательным пределом. Таким образом,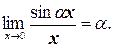

б) Поделим числитель и знаменатель дроби под знаком предела на х, после чего воспользуемся предыдущим пунктом:

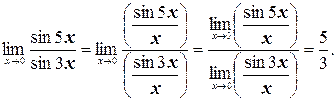
в) Сводя предел к первому замечательному пределу, сделаем замену у = х – 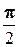. Тогда у ®0 при х ® 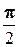, а х = у + 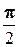, откуда:

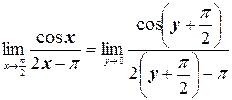
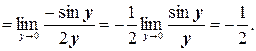
Во втором равенстве в этой цепочке мы использовали формулу приведения, а в последнем – первый замечательный предел.

г) Так как х ®0, то воспользуемся эквивалентностью №4:

.

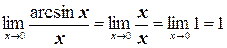Варианты заданий

№1.1. Найти пределы:

а) ;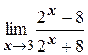

б) ;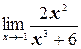

в) ;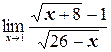

г) ;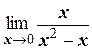

д) ;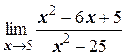

е) ;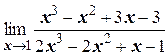

ж) ;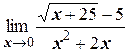

з) ;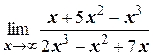

и) ;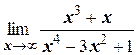

к) ;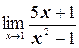

л) ;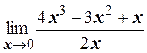

м) .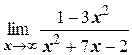

№1.2. Найти пределы:

а) ;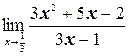

б) ;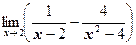

в) ;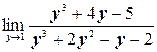

г) ;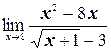

д) ;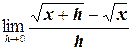

е) ;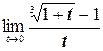

ж) ;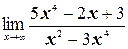

з) ;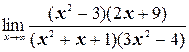

и) ;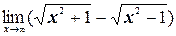

к) .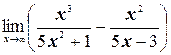

№1.3. Найти пределы:

а) ;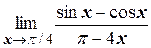

б) ;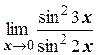

в) ;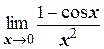

г) ;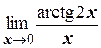

д) ;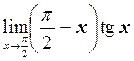

е) ;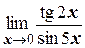

ж) ;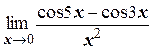

з)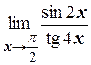

Контрольные вопросы