Найдем предел отношения двух многочленов, т.е. 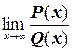 , где
, где
P (x) = a 0 xn + a 1 xn– 1 +…+an, Q (x) = b 0 xm + b 1 xm– 1 +…+bm. Преобразуем данную дробь следующим образом
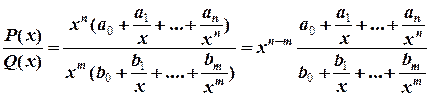
Таким образом, 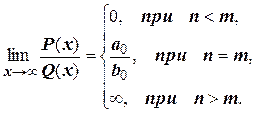
Первый замечательный предел: 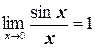
Второй замечательный предел: 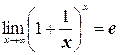 , где е постоянная, которая приблизительно равна 2,718281828…
, где е постоянная, которая приблизительно равна 2,718281828…
Часто если непосредственное нахождение предела какой-либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:
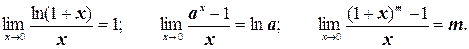
При решении многих задач используются следующие эквивалентности, верные при х ®0:
1. 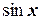 ~ х;
~ х;
2. 1–cos x ~ 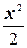 ;
;
3. tg x ~ x;
4. arcsin x ~ x;
5. arctg x ~ x;
6. ln (1+ x) ~ x;
7. ax –1 ~ x ln a;
8. 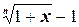 ~
~ 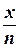 .
.
 2015-03-07
2015-03-07 896
896








