Пусть функция y = f (x) имеет производную в точке x 0. Тогда существует касательная к графику этой функции в точке М 0(x 0, у 0), уравнение которой имеет вид
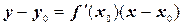 .
.
При этом 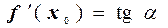 , где a – угол наклона этой касательной к положительному направлению оси ОХ (рис. 2.1).
, где a – угол наклона этой касательной к положительному направлению оси ОХ (рис. 2.1).
 |
Геометрически, чтобы провести касательную, надо к графику кривой приставить линейку так, чтобы она коснулась графика в выбранной точке.
Геометрический смысл: угловой коэффициент касательной, приведенной к графику функции y = f (x) в точке x 0 равен значению производной функции в этой точке.
Физический смысл: скорость тела равна первой производной координаты по времени:
V (t)= x / (t). (2.1)
Соответственно, вторая производная функции – скорость изменения скорости, т.е. ускорение:
a (t)= V / (t)= x // (t). (2.2)
Таблица производных
1. С ¢ = 0, где С –постоянная
2. (xm)¢ = mxm– 1
3. 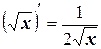
4. 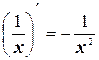
5. 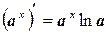
6. 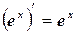
7. 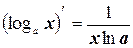
8. 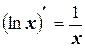
9. 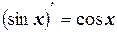
10. 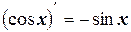
11. 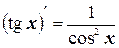
12. 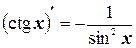
13. 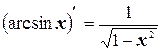
14. 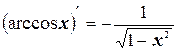
15. 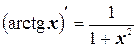
16. 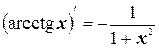
 2015-03-07
2015-03-07 914
914








