№1. Найти общий интеграл уравнения 6 ex cos2 y dx + ( 1 – 2 ex) ctg y dy= 0.
Решение. Разделим переменные в данном уравнении, поделив обе его части на выражение cos2 y ( 1 – 2 ex):
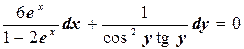 .
.
Интегрируя обе части уравнения, имеем
– 3ln | 1 – 2 ex |+ ln|tg y | = ln | C |, C 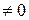
(поскольку C – произвольная постоянная, то для удобства дальнейших преобразований мы заменили С на ln| C |). Отсюда
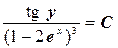 или
или 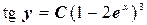 .
.
Получили общий интеграл данного уравнения. При делении на cos2 y( 1 – 2 ex) мы могли потерять решения 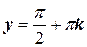 , k – целое число, x = – ln2, но они содержатся в общем интеграле, если подставить значение С = 0.
, k – целое число, x = – ln2, но они содержатся в общем интеграле, если подставить значение С = 0.
№2. Решить уравнение 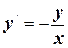
Решение. Запишем уравнение в виде 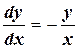 . Разделяя переменные, будем иметь
. Разделяя переменные, будем иметь 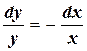 и, следовательно,
и, следовательно, 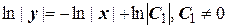 .
.
После потенцирования получим общее решение
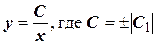 (10.10)
(10.10)
При делении на у мы могли потерять решение у = 0, но последнее содержится в формуле (10.10) при С = 0.
№3. Найти частное решение ДУ 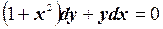 при начальных условиях y ( 1 )= 1.
при начальных условиях y ( 1 )= 1.
Решение. Разделяя переменные, приведем данное уравнение к виду 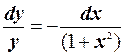 . Интегрируя обе части уравнения, получим
. Интегрируя обе части уравнения, получим 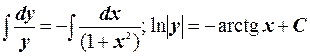 . Это и есть общий интеграл исходного уравнения.
. Это и есть общий интеграл исходного уравнения.
Подставим теперь начальные условия и найдем произвольную постоянную С: 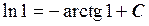 , т.е.
, т.е. 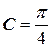 . Следовательно,
. Следовательно, 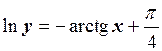 , откуда получаем искомое частное решение
, откуда получаем искомое частное решение 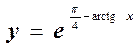 .
.
 2015-03-07
2015-03-07 444
444








