2015-03-27
1298
Определение 7.7. Комплексное число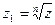 
называется корнем n -й степени из z, если z = z 1 n.
Из определения следует, что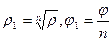 
. Так как аргумент комплексного числа определен не однозначно, можно получить n различных значений для аргумента z1: 
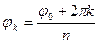, где φ0 – одно из значений arg z, а k = 1, 2,…, n -1. Окончательно формулу, задающую все значения 
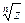, можно записать в виде:
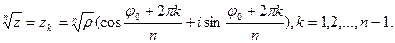(7.3)
Пример. Число z = 16 можно представить в тригонометрической форме следующим образом: z = 16(cos0 + i sin0). Найдем все значения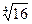 
:
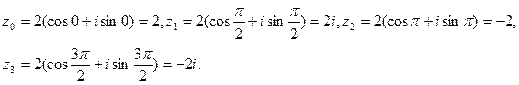
Показательная форма комплексного числа.
Введем еще одну форму записи комплексного числа. На множестве комплексных чисел существует связь между тригонометрическими и показательными функциями, задаваемая формулой Эйлера:
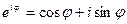, (7.4)
справедливость которой будет доказана в дальнейшем. Используя эту формулу, можно получить из (7.1) еще один вид комплексного числа: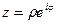 
(7.5)
Определение 7.8. Запись вида (7.5) называется показательной формой записи комплексного числа.
Представление (7.5) позволяет легко интерпретировать с геометрической точки зрения операции умножения, деления, возведения в степень и извлечения корня, используя известные свойства показательной функции.
|
|
|
Лекция 8.
Многочлены и их корни. Теорема Безу. Основная теорема алгебры. Разложение многочлена на линейные множители в поле комплексных чисел. Простые и кратные корни многочлена. Разложение многочлена с действительными коэффициентами на линейные и квадратичные множители. Рациональные функции. Деление многочленов, выделение целой части рациональной функции. Правильные рациональные функции, их разложение на простейшие.
Рассмотрим в комплексной области многочлен, то есть функцию вида
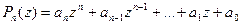, (8.1)
где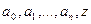 
- комплексные числа. Числа 
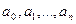называются коэффициентами многочлена, а натуральное число n – его степенью.
Определение 8.1. Два многочлена Pn (z) и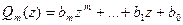 
равны тогда и только тогда, когда m=n, a0 = b0, a1 = b1,…, an = bn.
Определение 8.2. Число z0 называется корнем многочлена (8.1), если Pn (z0) = 0.
Теорема 8.1 (теорема Безу). Остаток от деления многочлена Pn(z) на z – z0 (z0 – не обязательно корень многочлена) равен P(z0).
Доказательство. Разделив P(z) на z – z0, получим: P(z) = Q(z)(z – z0) + r, где число r – остаток от деления, а Q(z) – многочлен степени, меньшей n. При подстановке в это равенство z = z0 найдем, что r = P(z0), что и требовалось доказать.
Теорема 8.2 (основная теорема алгебры). Всякий многочлен в комплексной области имеет корень (без доказательства).
