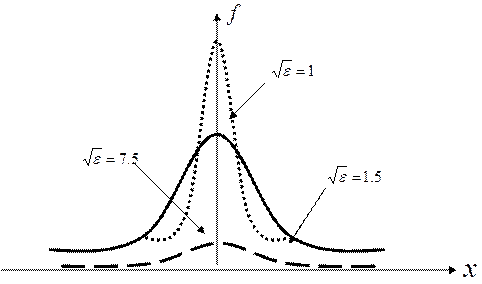Центрированные нормальные кривые распределения

Покажем, что при 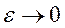эта функция стремится к d - функции. Заметим, что 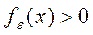, поэтому, при любых a и b

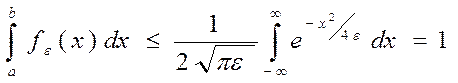1) (18)

(Известно из нормального распределения)

Сделав замену 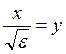(эта замена переменных, чтобы отнормировать кривую), мы видим, что

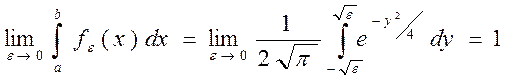(19)

Далее, для гауссова импульса для любого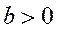

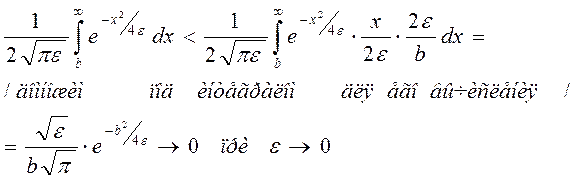(20)

(Пояснение: безразмерная величина ,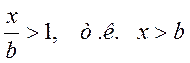

интегрирование от b до ¥, x – переменная интегрирования, поэтому правый интеграл больше левого).

Таким образом, интегралы (20) по любому промежутку из 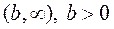, стремятся к нулю.

Аналогично, при (-¥, a ), a < 0. Таким образом 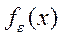есть дельтаобразная последовательность и значит, что

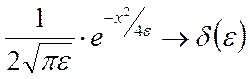
(21)