Определение 1. Точка 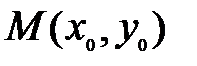 называется точкой максимума функции
называется точкой максимума функции 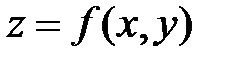 , если существует окрестность точки М такая, что для всех точек
, если существует окрестность точки М такая, что для всех точек 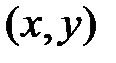 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 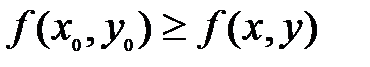 .
.
Определение 2. Точка 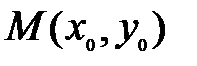 называется точкой минимума функции
называется точкой минимума функции 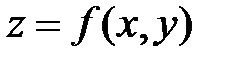 , если существует окрестность точки М такая, что для всех точек
, если существует окрестность точки М такая, что для всех точек 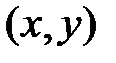 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 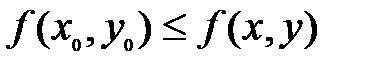 .
.
Максимумы и минимумы функции называются локальными экстремумами, а 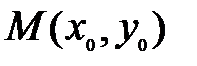 - точкой локального экстремума.
- точкой локального экстремума.
Замечание 1. В силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке 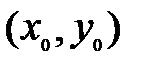 сравнивается с ее значением в точках, достаточно близких к
сравнивается с ее значением в точках, достаточно близких к 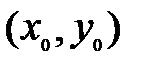 . В области определения функция может иметь несколько экстремумов или не иметь ни одного.
. В области определения функция может иметь несколько экстремумов или не иметь ни одного.
Сформулируем необходимое условие экстремума функции.
Теорема 1 (необходимое условие экстремума). Пусть дифференцируемая функция 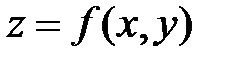 имеет в точке
имеет в точке 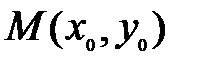 экстремум. Тогда частные производные первого порядка
экстремум. Тогда частные производные первого порядка 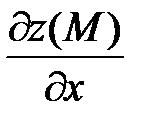 и
и 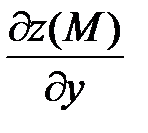 в этой точке равны нулю.
в этой точке равны нулю.
|
|
|
Точки, в которых выполнены необходимые условия экстремума функции 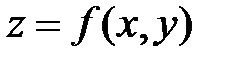 , т.е. частные производные первого порядка обращаются в нуль (или не существуют), называются критическими или стационарными. Еще их называют точками «подозрительными на экстремум»
, т.е. частные производные первого порядка обращаются в нуль (или не существуют), называются критическими или стационарными. Еще их называют точками «подозрительными на экстремум»
Замечание 2. Равенство нулю частных производных выражает лишь необходимое, но недостаточное условие существования экстремума функции нескольких переменных.
Поэтому требуются еще достаточные условия существования экстремума.
Теорема 2 (достаточные условия существования экстремума). Пусть функция 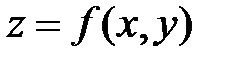 : а) определена в некоторой окрестности критической точки
: а) определена в некоторой окрестности критической точки 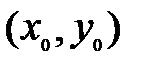 в которой
в которой 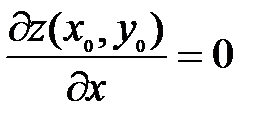 и
и 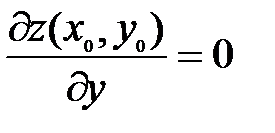 ; б) имеет в этой точке непрерывные частные производные второго порядка
; б) имеет в этой точке непрерывные частные производные второго порядка 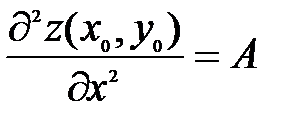 ,
, 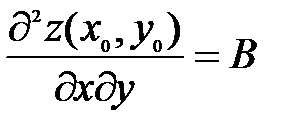 ,
, 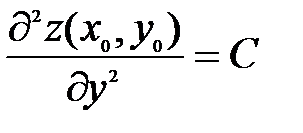 . Тогда, если
. Тогда, если
1. 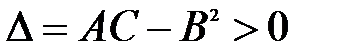 , то в точке
, то в точке 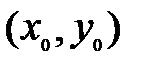 функция
функция 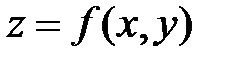 имеет
имеет
экстремум, причем если 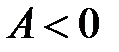 - максимум, если
- максимум, если 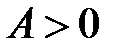 - минимум;
- минимум;
2. 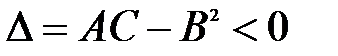 , то функция
, то функция 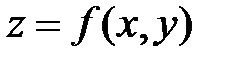 экстремума не имеет;
экстремума не имеет;
3. 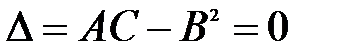 , то вопрос о наличии экстремума остается открытым.
, то вопрос о наличии экстремума остается открытым.
Исследование функции двух переменных на локальный экстремум проводится по следующему алгоритму:
1. Найти частные производные функции 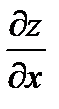 ,
, 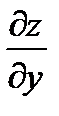 и приравнять их к нулю:
и приравнять их к нулю:
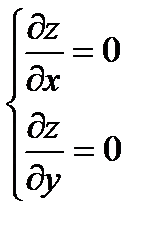 .
.
2. Решить полученную систему уравнений и найти критические точки функции.
3. Найти частные производные второго порядка 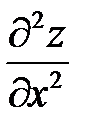 ,
, 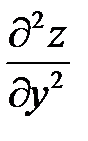 ,
, 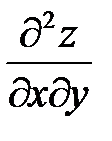 .
.
4. Вычислить значения частных производных второго порядка в каждой критической точке.
5. С помощью достаточных условий сделать вывод о наличии экстремумов.
6. Найти экстремумы, т.е. экстремальные значения функции.
Рассмотрим типичные примеры для решения которых используются приведенные понятия, определения и теоремы:
Пример 1. Исследовать на экстремум функцию 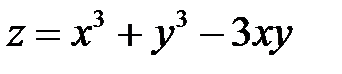 .
.
Решение.
1. Находим частные производные
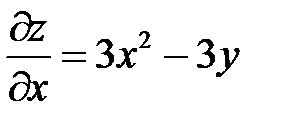 ;
; 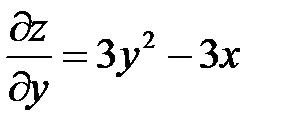 .
.
Приравнивая их к нулю, получим, 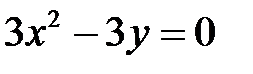 ,
, 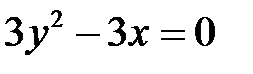 .
.
|
|
|
2. Решаем систему 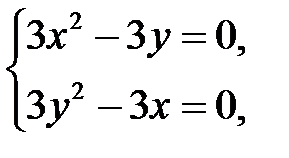

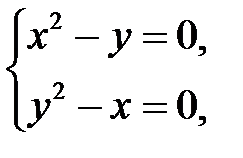

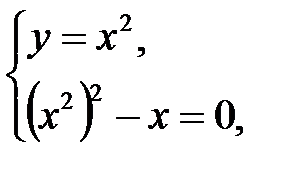

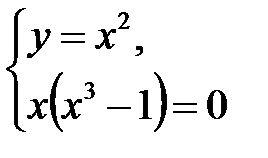 из последней системы, получим
из последней системы, получим 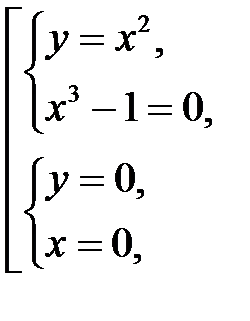

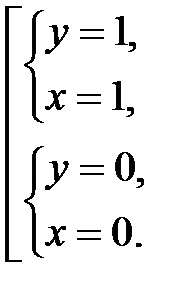
Следовательно, критические точки: 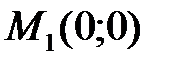 и
и 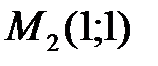 .
.
3. Находим частные производные второго порядка:
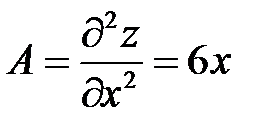 ,
, 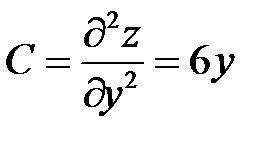 ,
, 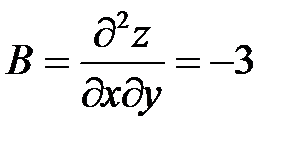 .
.
4. Вычисляем значения этих производных в каждой критической точке:
1) 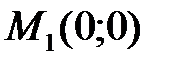 :
: 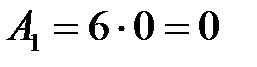 ;
; 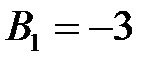 ;
; 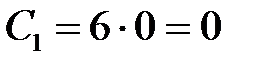 .
.
2) 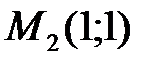 :
: 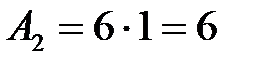 ;
; 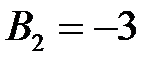 ;
; 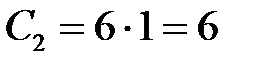 .
.
5. Проверяем в каждой точке выполнение достаточного условия
1) 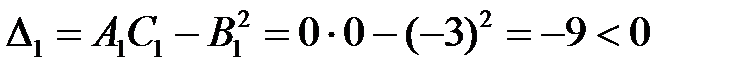 – экстремума нет.
– экстремума нет.
2) 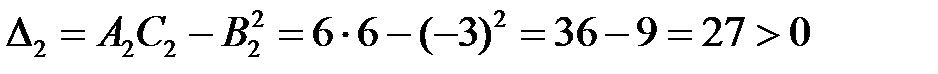 – экстремум есть, причем
– экстремум есть, причем 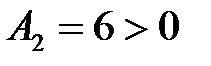 , следовательно, в точке
, следовательно, в точке 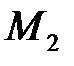 минимум.
минимум.
6. Находим экстремальное значение функции 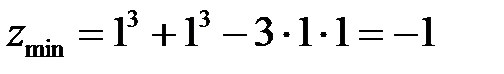 .
.
Ответ: 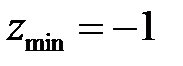 .
.
Пример 2. Исследовать на экстремум функцию 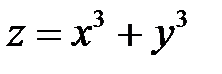 .
.
Решение: Проведя исследование по той же схеме, получим:
1. 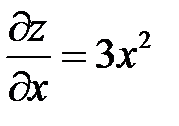 ;
; 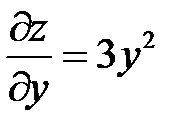 .
.
2. Решим систему 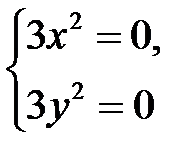 , которая имеет единственное решение
, которая имеет единственное решение 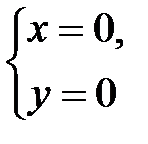 .
.
Следовательно, критическая точка 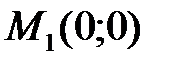 .
.
3. Находим частные производные второго порядка:
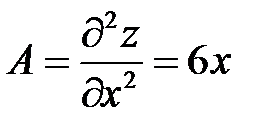 ,
, 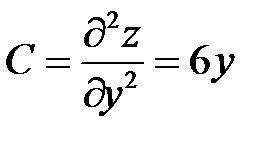 ,
, 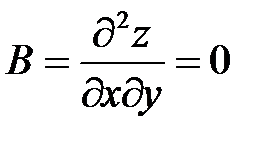 .
.
4. Значения частных производных в критической точке равны: 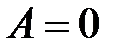 ,
, 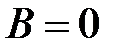 ,
, 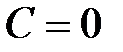 .
.
5. Проверим выполнение достаточного условия 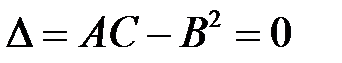 , следовательно, вопрос о наличии экстремума открыт.
, следовательно, вопрос о наличии экстремума открыт.
Проанализируем данную функцию 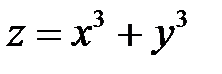 :
:
1) в критической точке 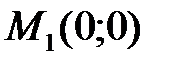
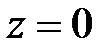 ;
;
2) в любой окрестности этой точки она принимает значения разных знаков.
Очевидно, что экстремума в точке 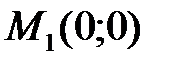 данная функция не имеет.
данная функция не имеет.
Ответ: экстремума нет.
Пример 3. Исследовать на экстремум функцию 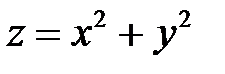 .
.
Решение: Проведя исследование аналогично предыдущему примеру, получим, что данная функция имеет критическую точку 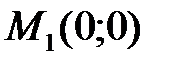 и достаточные условия дают
и достаточные условия дают 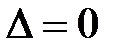 .
.
Проанализируем данную функцию 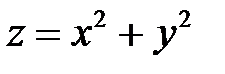 :
:
1) в критической точке 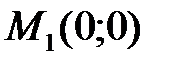
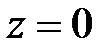 ;
;
2) в любой окрестности этой точки она принимает положительные значения.
Очевидно, что в точке 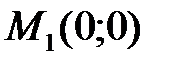 данная функция имеет минимум.
данная функция имеет минимум.
Ответ: 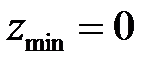 .
.
Пример 4. Производится два вида продукции в количествах x и y соответственно. Цена продукции 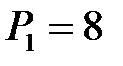 ,
, 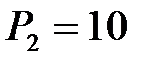 . Найти максимум прибыли, если функция затрат имеет вид:
. Найти максимум прибыли, если функция затрат имеет вид: 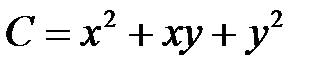 .
.
Решение. Составим функцию прибыли
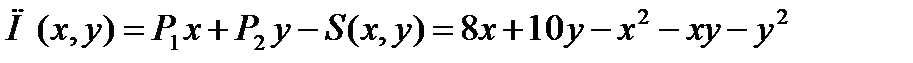 .
.
Исследуем полученную функцию двух переменных на экстремум.
1. Находим частные производные:
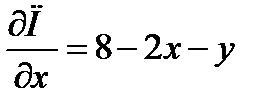 ,
, 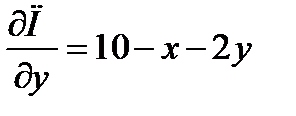 .
.
2. Составим систему 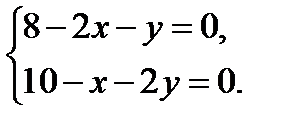
Данная система имеет единственное решение 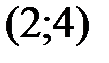 .
.
3. Критическая точка 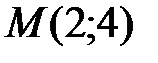 .
.
4. Находим частные производные второго порядка:
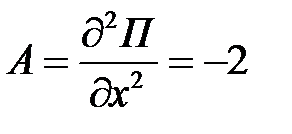 ,
, 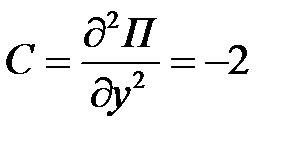 ,
, 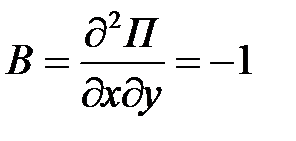 .
.
5. Значения частных производных в критической точке равны: 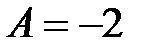 ,
, 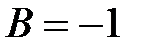 ,
, 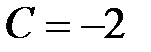 .
.
6. Проверим выполнение достаточного условия 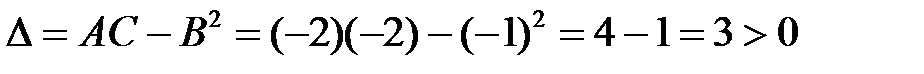 , следовательно экстремум есть, так как
, следовательно экстремум есть, так как 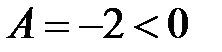 , то точка критическая точка
, то точка критическая точка 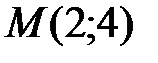 является точкой максимума.
является точкой максимума.
7. Находим экстремальное значение функции прибыли 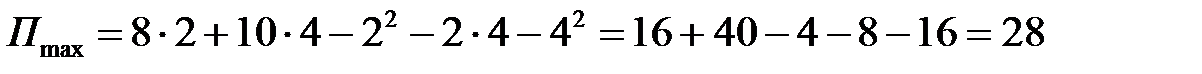 .
.
Ответ: 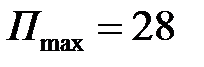 .
.
 2015-03-07
2015-03-07 12137
12137
