Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию.
Пусть имеется функция 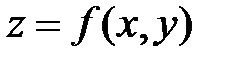 , аргументы x и y которой удовлетворяют условию
, аргументы x и y которой удовлетворяют условию 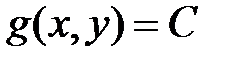 , называемому уравнением связи.
, называемому уравнением связи.
Определение 1. Точка 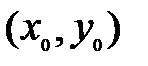 называется точкой условного максимума или минимума, если существует такая ее окрестность, что для всех точек
называется точкой условного максимума или минимума, если существует такая ее окрестность, что для всех точек 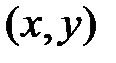 из этой окрестности, удовлетворяющих условию
из этой окрестности, удовлетворяющих условию 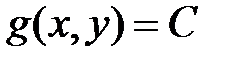 , выполняется неравенство
, выполняется неравенство 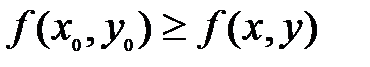 или
или 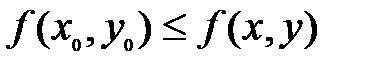 .
.
Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Допустим, уравнение связи 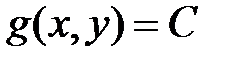 удалось разрешить относительно одной из переменных, например выразить y через x, т.е
удалось разрешить относительно одной из переменных, например выразить y через x, т.е 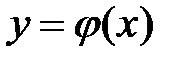 . Подставив полученное выражение в функцию двух переменных, получим
. Подставив полученное выражение в функцию двух переменных, получим 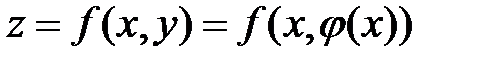 , т.е. функцию одной переменной. Ее экстремум и будет условным экстремумом функции
, т.е. функцию одной переменной. Ее экстремум и будет условным экстремумом функции 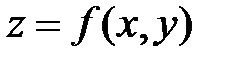 .
.
Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.
Рассмотрим функцию трех переменных
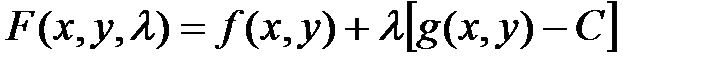 .
.
Эта функция называется функцией Лагранжа, а 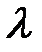 - множителем (коэффициентом) Лагранжа. Доказывается следующая теорема:
- множителем (коэффициентом) Лагранжа. Доказывается следующая теорема:
Теорема 1. Если точка 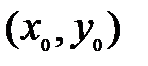 является точкой условного экстремума функции
является точкой условного экстремума функции 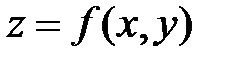 при условии
при условии 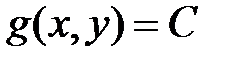 , то существует значение
, то существует значение 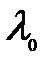 такое, что точка
такое, что точка 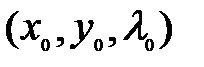 является точкой экстремума функции
является точкой экстремума функции 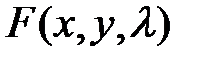 .
.
Таким образом, для нахождения условного экстремума функции 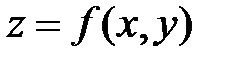 при условии
при условии 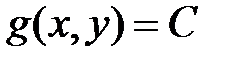 требуется найти решение следующей системы:
требуется найти решение следующей системы:
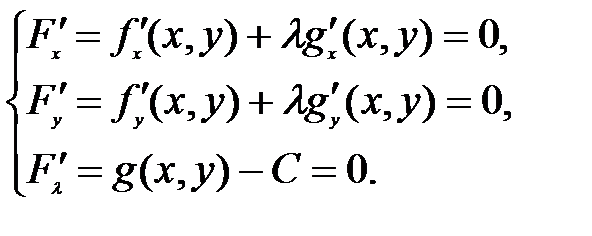
Последнее из этих уравнений совпадает с уравнением связи. Данная система выражает необходимые условия Лагранжа условного экстремума.
Из этой системы уравнений находят критические точки условного экстремума.
Определение 2. Точка 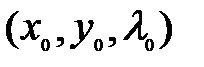 называется критической точкой функции Лагранжа, если
называется критической точкой функции Лагранжа, если 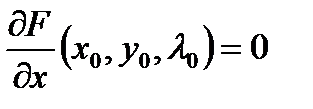 ,
, 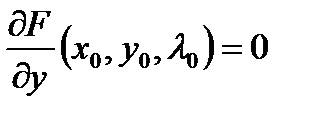 ,
, 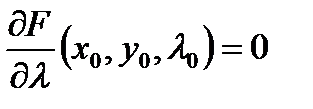 (или не существуют).
(или не существуют).
Для исследования критических точек на экстремум вычисляем в полученных точках значения 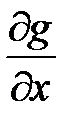 ,
, 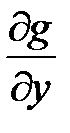 ,
, 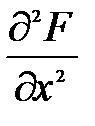 ,
, 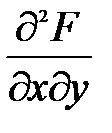 ,
, 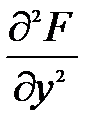 и составляем определитель
и составляем определитель
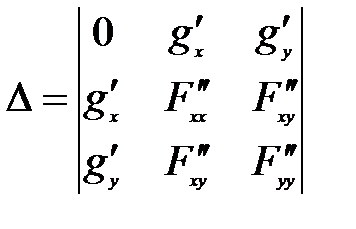 .
.
Тогда достаточные условия условного экстремума запишутся в следующем виде:
1. Если  , то функция
, то функция 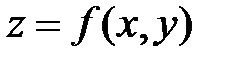 имеет в точке
имеет в точке 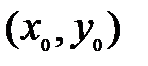 условный минимум;
условный минимум;
2. если 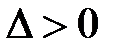 - то условный максимум.
- то условный максимум.
Исследование функции на условный экстремум с помощью метода множителей Лагранжа проводится по следующему алгоритму:
1. Составить функцию Лагранжа
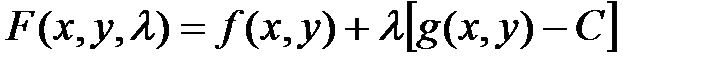 .
.
2. Найти частные производные 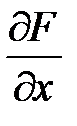 ,
, 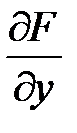 ,
, 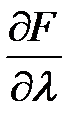 и приравнять их к нулю, т.е. составить необходимые условия экстремума функции Лагранжа.
и приравнять их к нулю, т.е. составить необходимые условия экстремума функции Лагранжа.
3. Решить систему уравнений
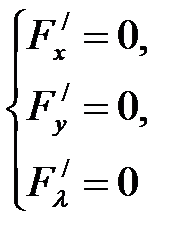
и найти критические точки.
4. Найти частные производные:
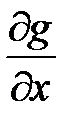 ,
, 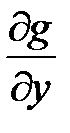 ,
, 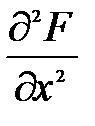 ,
, 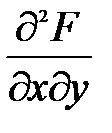 ,
, 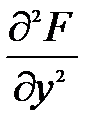 .
.
5. Вычислить значения найденных частных производных в каждой критической точке.
6. Из найденных значений составить определитель  .
.
7. С помощью достаточных условий сделать вывод о характере экстремальной точки.
8. Найти значения функции в точках условного экстремума.
1. Находим производную 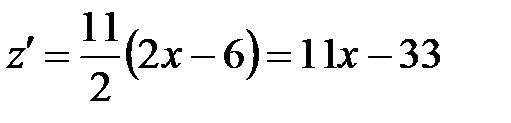 .
.
Решение. Из уравнения связи 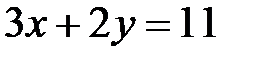 выразим переменную y через переменную x и подставим полученное выражение
выразим переменную y через переменную x и подставим полученное выражение 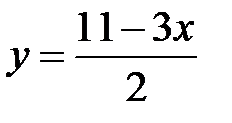 в функцию z. Получим
в функцию z. Получим 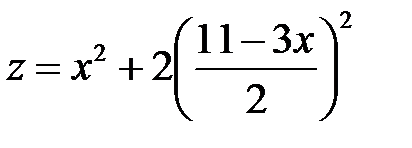 или
или 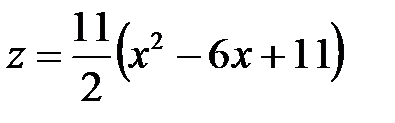 . Эта функция одного переменного. Исследуем ее на экстремум:
. Эта функция одного переменного. Исследуем ее на экстремум:
Пример 1. Исследовать на экстремум функцию 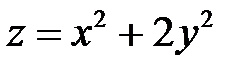 при условии
при условии 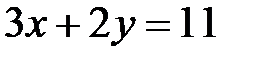 .
.
Рассмотрим типичные примеры для решения которых используются приведенные понятия, определения и теоремы: Геометрический смысл условий Лагранжа. Линия 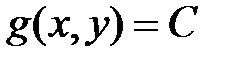 пунктирная (рис.1), линии уровня
пунктирная (рис.1), линии уровня 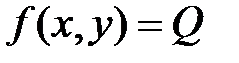 функции
функции 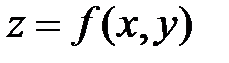 – сплошные. В точке условного экстремума линия уровня функции
– сплошные. В точке условного экстремума линия уровня функции 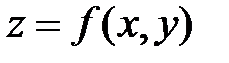 касается линии
касается линии 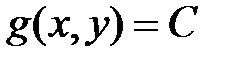 .
.
2. Приравняем производную к нулю, получим уравнение 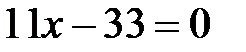 , решением которого служит значение
, решением которого служит значение 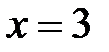 .
.
3. Находим вторую производную 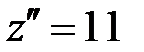 , так как ее значение в критической точке больше нуля, то по второму достаточному условию экстремума делаем вывод, что
, так как ее значение в критической точке больше нуля, то по второму достаточному условию экстремума делаем вывод, что 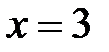 – точка минимума функции
– точка минимума функции 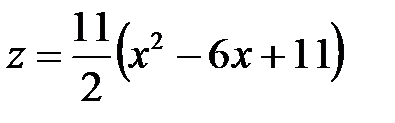 .
.
При этом соответствующее значение функции 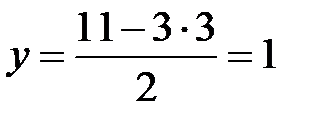 . Таким образом,
. Таким образом, 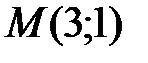 – точка условного экстремума (минимума) и
– точка условного экстремума (минимума) и 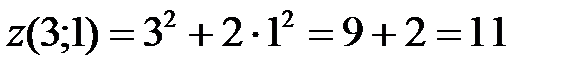 .
.
Ответ: 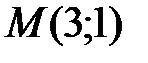 – точка условного минимума;
– точка условного минимума; 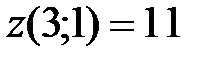 .
.
Пример 2. Найти экстремумы функции 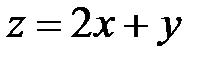 при условии
при условии 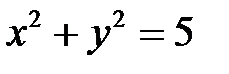 .
.
Решение. Используем метод множителей Лагранжа. Уравнение связи имеет вид:
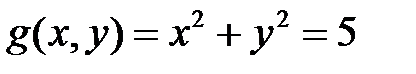 .
.
1. Составим функцию Лагранжа: 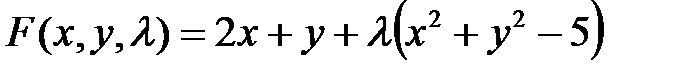 ;
;
2. Находим частные производные: 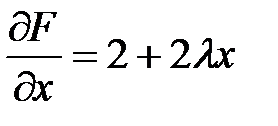 ,
, 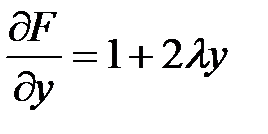 ,
, 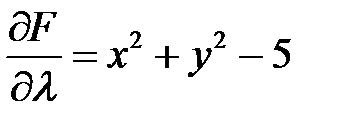 .
.
3. Приравняем частные производные к нулю, получим систему:
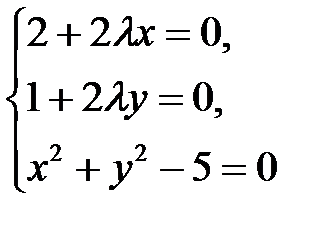
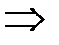
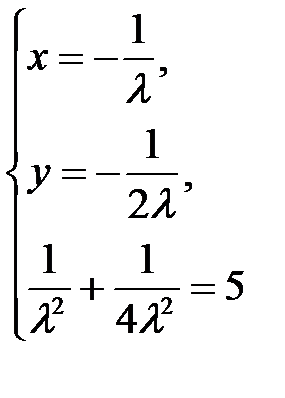
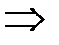
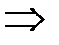
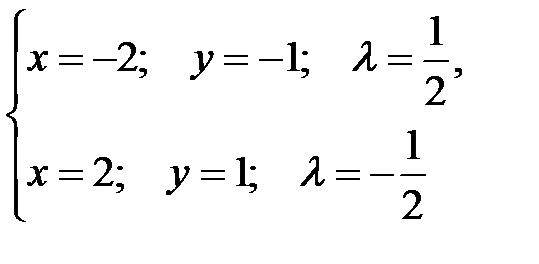
Таким образом, получили две критические точки 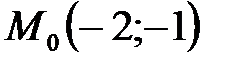 при
при 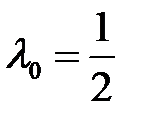 и
и 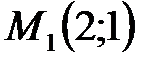 при
при 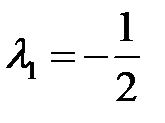 .
.
4. Находим следующие производные: 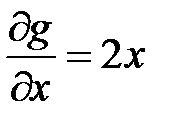 ;
; 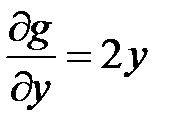 ;
; 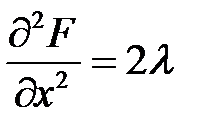 ,
, 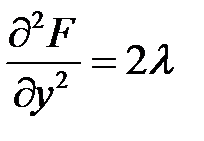 ;
; 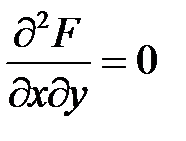 .
.
5. Вычисляем значения найденных частных производных в каждой критической точке:
1) 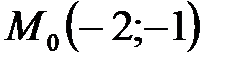 при
при 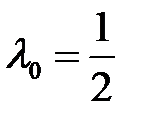 :
:
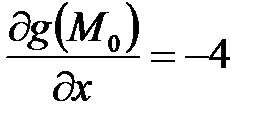 ;
; 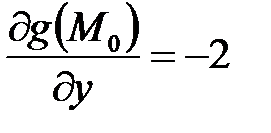 ;
; 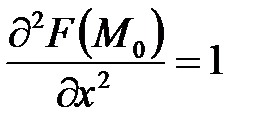 ,
, 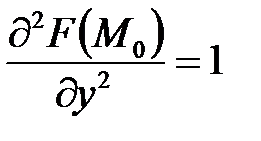 ;
; 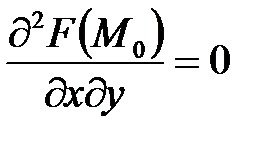 ;
;
2) 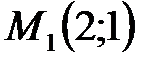 при
при 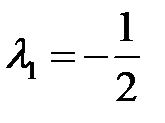 :
:
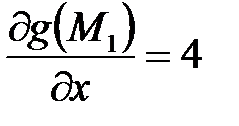 ;
; 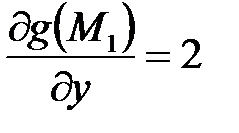 ;
; 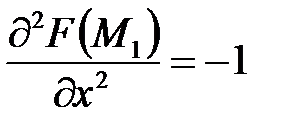 ,
, 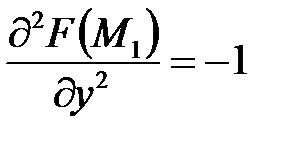 ;
; 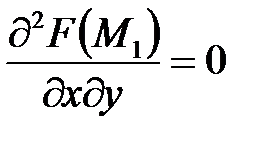 .
.
6. Составляем из найденных значений определитель:
1) 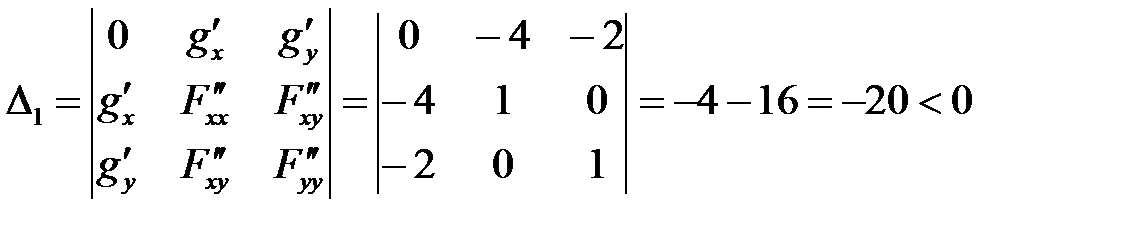 ,
,
2) 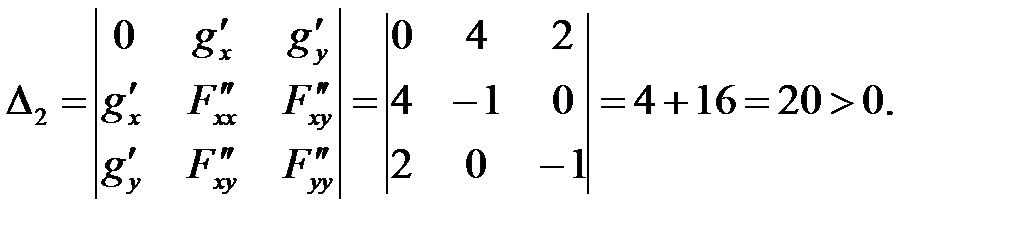
7. Проверяем в каждой точке выполнение достаточного условия. Так как 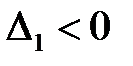 , то в точке
, то в точке 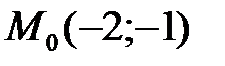 условный минимум; а из того, что
условный минимум; а из того, что 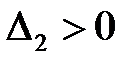 делаем вывод, что в точке
делаем вывод, что в точке 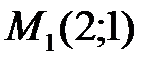 условный максимум.
условный максимум.
8. Вычисляем значения функции в критических точках: 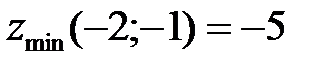 ,
, 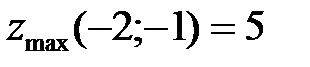 .
.
Ответ: 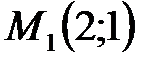 при
при 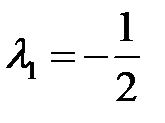 - точка условного максимума,
- точка условного максимума, 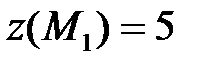 ;
;
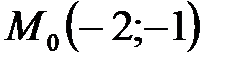 при
при 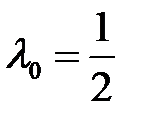 – точка условного минимума,
– точка условного минимума, 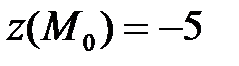 .
.
Пример 3. Найти экстремумы функции 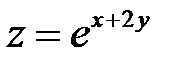 при условии, что
при условии, что 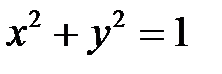 .
.
Решение. Используем метод множителей Лагранжа.
1. Составим функцию Лагранжа: 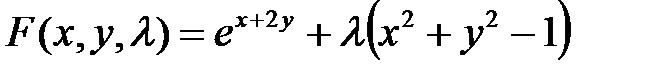 ;
;
2. Находим частные производные: 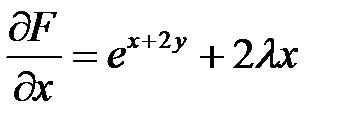 ,
, 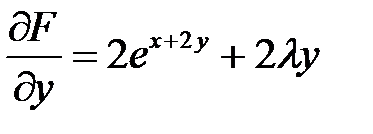 ,
, 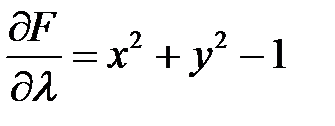 .
.
3. Приравняем частные производные к нулю, получим систему:
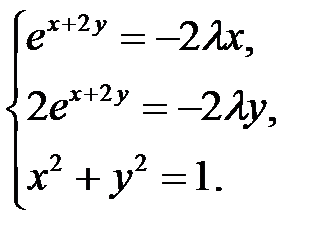
Из первых двух уравнений системы находим 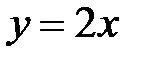 ; подставляем это выражение в третье уравнение, получаем два решения
; подставляем это выражение в третье уравнение, получаем два решения 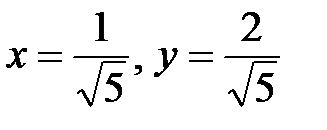 и
и 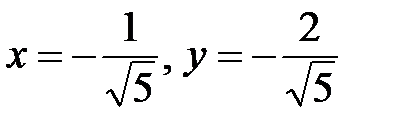 . Таким образом, получили две критические точки
. Таким образом, получили две критические точки 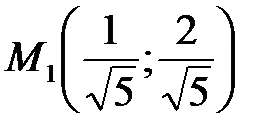 при
при 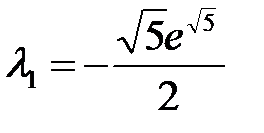 и
и 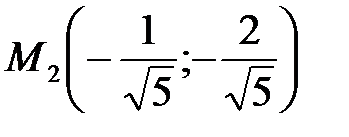 при
при 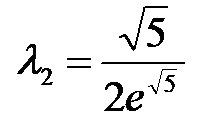 .
.
4. Находим следующие производные: 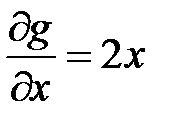 ;
; 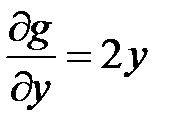 ;
; 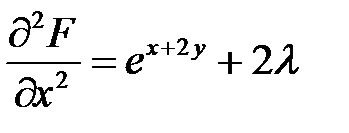 ,
, 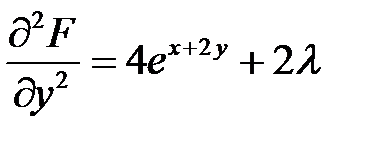 ;
; 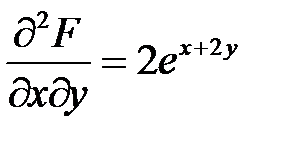 .
.
5. Вычисляем значения найденных частных производных в каждой критической точке:
1) 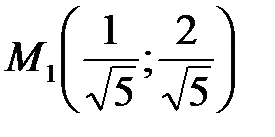 при
при 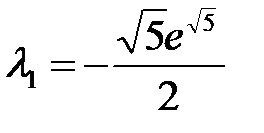 :
:
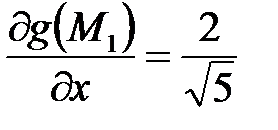 ;
;  ;
; 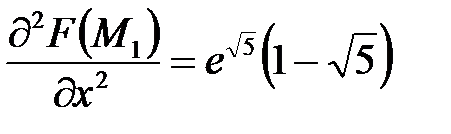 ,
, 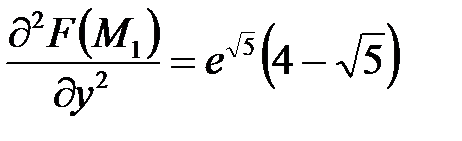 ;
; 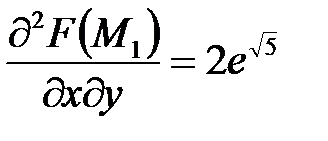 ;
;
2) 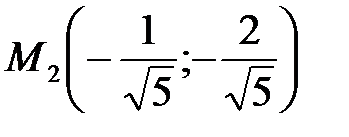 при
при 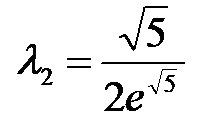 :
:
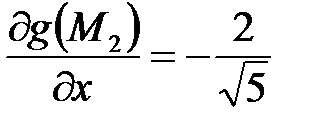 ;
; 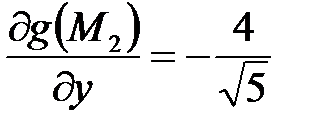 ;
; 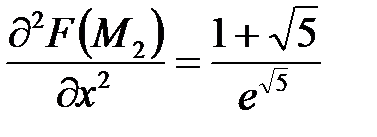 ,
, 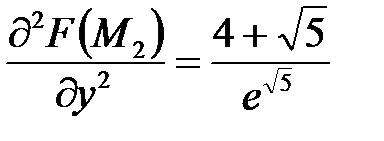 ;
; 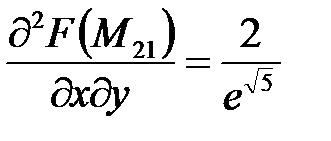 .
.
6. Составляем из найденных значений определитель:
1) 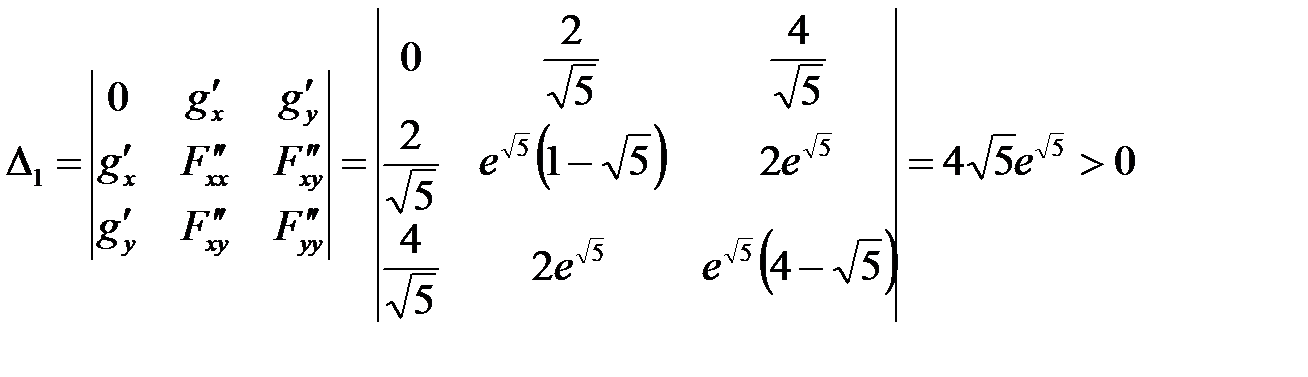 ,
,
2) 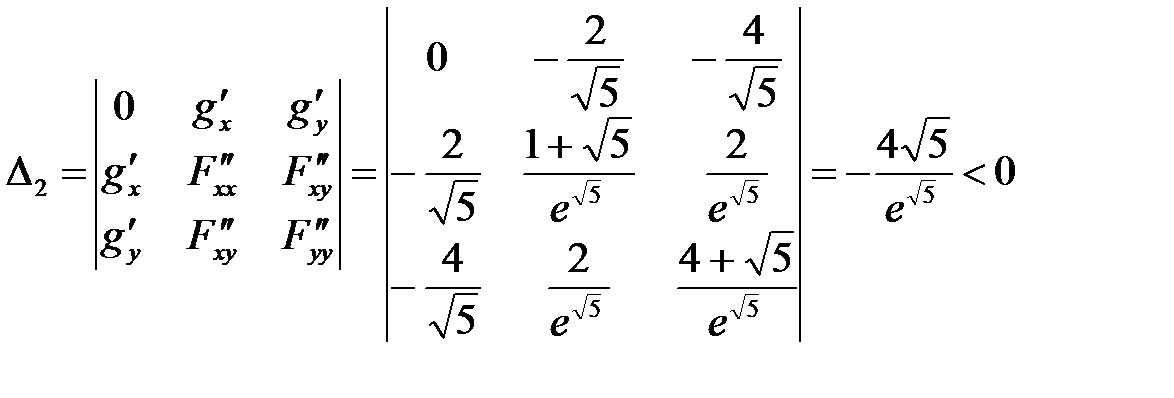 .
.
7. Проверяем в каждой точке выполнение достаточного условия. Так как 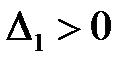 , то в точке
, то в точке 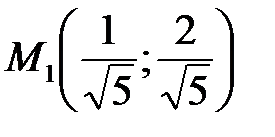 условный максимум; а из того, что
условный максимум; а из того, что 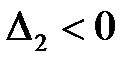 делаем вывод, что в точке
делаем вывод, что в точке 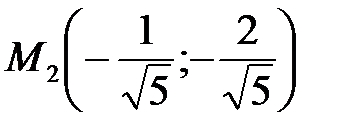 условный минимум.
условный минимум.
8. Вычисляем значения функции в критических точках: 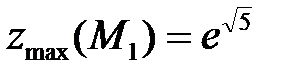 ,
, 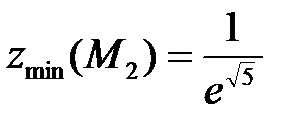 .
.
Ответ:
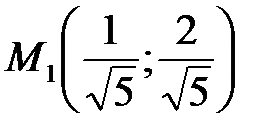 при
при 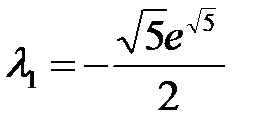 - точка условного максимума,
- точка условного максимума, 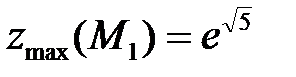 ;
;
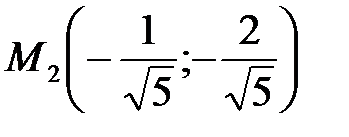 при
при 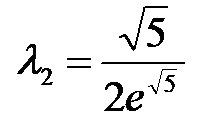 – точка условного минимума,
– точка условного минимума, 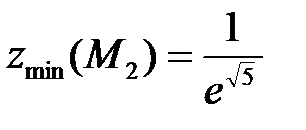 .
.
 2015-03-07
2015-03-07 18372
18372
