Определение 5.3. Циркуляцией Ц векторного поля а = а(М) называется линейный интеграл, взятый вдоль замкнутой ориентированной кривой L. Таким образом, по определению
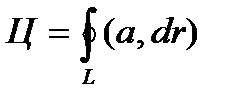
где символ 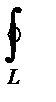 означает интеграл по замкнутой кривой L.
означает интеграл по замкнутой кривой L.
Если векторное поле а = а(М) задано в координатой форме
a = P(x,y,z)i + Q(x,y,z)j + R(x,y,z)k
то циркуляция векторного поля будет равна
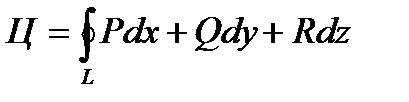
За положительное направление обхода замкнутой кривой L будем считать направление, при котором область, ограниченная этой кривой, будет оставаться слева.
Пример 5.5. Вычислить циркуляцию векторного поля 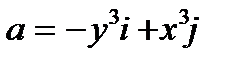 вдоль эллипса L:
вдоль эллипса L: 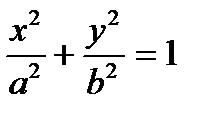 .
.
Решение. По определению циркуляции имеем
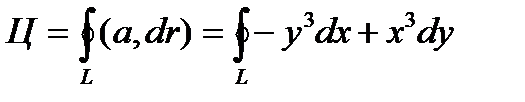 (5.4)
(5.4)
Параметрические уравнения данного эллипса имеют вид (рис. 5.3)
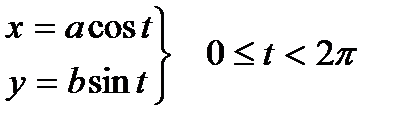 (5.5)
(5.5)
отсюда
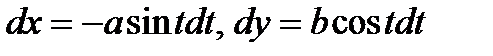 (5.6)
(5.6)
Подставляя (5.5) и (5.6) в (5.4), получим
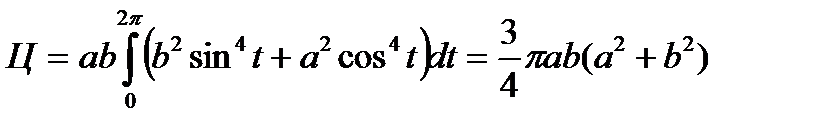
так как
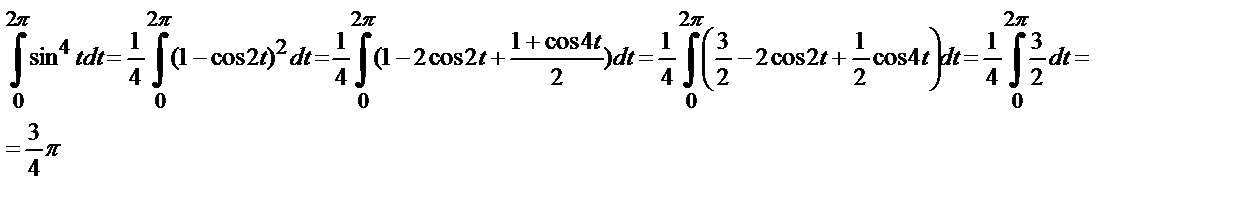 аналогично находим, что
аналогично находим, что
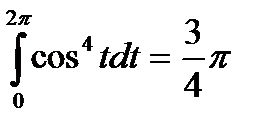
Пример 5.6. Вычислить циркуляцию векторного поля
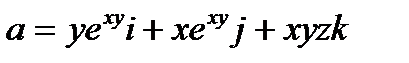
вдоль линии L, получаемой пересечением конуса x2 + y2 = (z-1)2 с координатными плоскостями (р 11.4)
Решение. Линия L состоит из двух отрезков ВС и СА, расположенных на координатных плоскостях YOZ и XOZ соответственно и 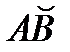 окружности
окружности 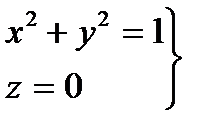 . Поэтому циркуляция данного векторного поля будет равна
. Поэтому циркуляция данного векторного поля будет равна
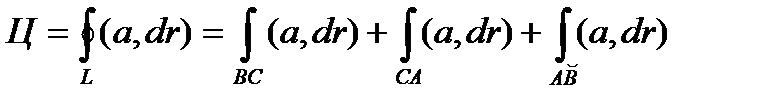
1. На отрезке ВС имеем
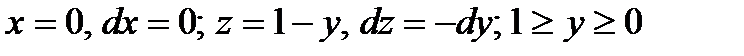
следовательно,
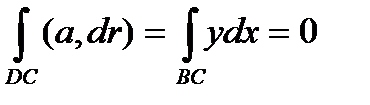
2. на отрезке СА имеем
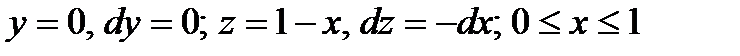
следовательно
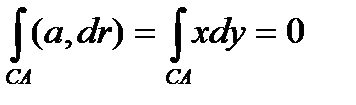
3. На дуге 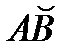 окружности
окружности 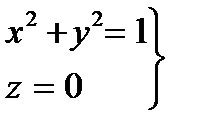 имеем z = 0, dz = 0, и значит
имеем z = 0, dz = 0, и значит
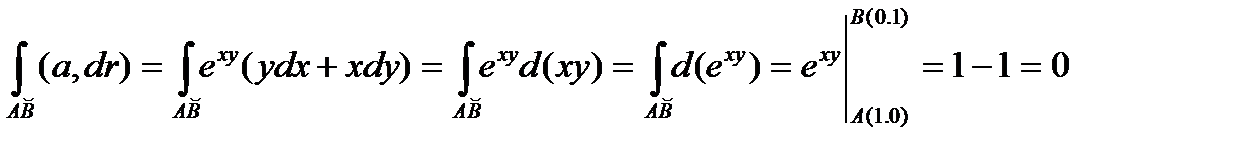
Искомая циркуляция векторного поля равна нулю.
Пример 5.7. Вычислить циркуляцию векторного поля a = xyi + yzj + xzk, если
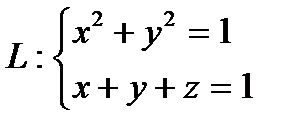
Решение. Имеем 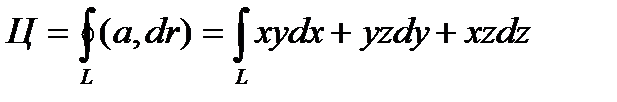
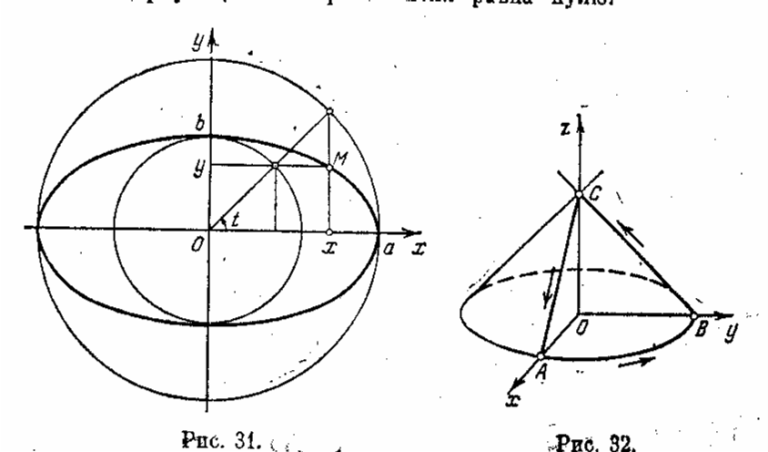
Линия L есть эллипс, получающийся в результате сечения цилиндра x2 + y2 = 1 плоскостью x + y + z = 1. Найдем параметрические уравнения этой линии. Проекция любой точки линии на плоскость ХОУ находится на окружности x2 + y2 = 1. Отсюда получаем x = cost, y = sint. Но
Рис. 5.3 Рис. 5.4
эллипс лежит на плоскости x + y + z = 1, откуда z = 1 - x - y или z = 1 - cost - sint. Следовательно, параметрические уравнения линии L:
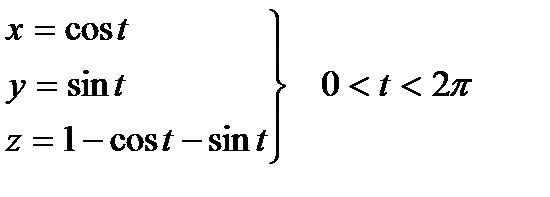
Отсюда находим
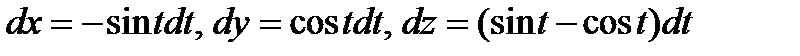
И, значит, циркуляция будет равна
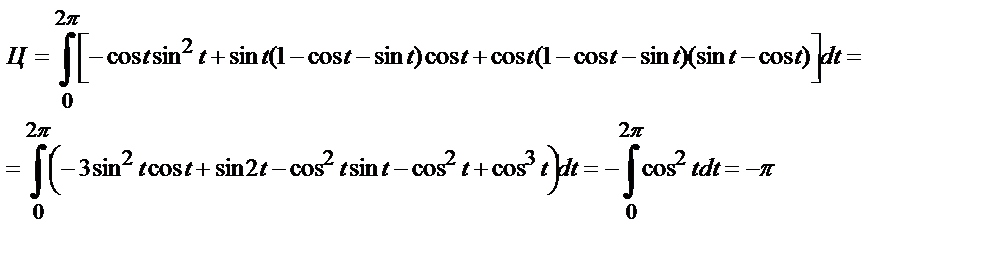
 2015-03-07
2015-03-07 22628
22628








