Доказательство. Фиксируем m и обозначим к-ю частичную сумму ряда через

Фиксируем m и обозначим к-ю частичную сумму ряда через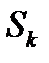

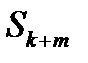
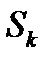
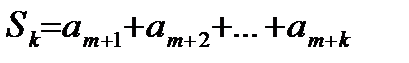
(15.6)

Тогда очевидно:

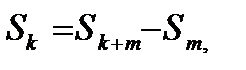(15.7)

Где:

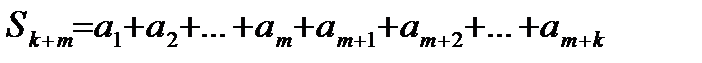
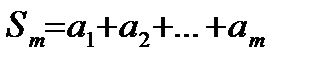
Если ряд (15.2) сходится то 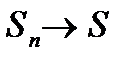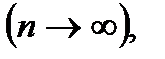то при неограниченном возрастании k существует конечный предел S 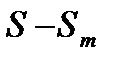(15.7)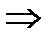 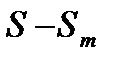является конечным для суммы 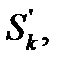что означает сходимость ряда (15.5). Обратно, если дано, что сходится ряд (15.5), так что 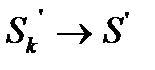то перепишим равенство (15.6), полагая в нем k=n-m(n>m), так: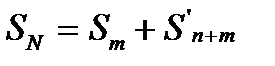

Отсюда вытекает, что при неограниченном возрастании n частная сумма 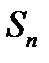имеет предел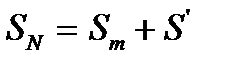

То есть сходиться ряд (15.2).