Пусть задана некоторая бесконечная последовательность чисел

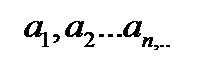 (15.1)
(15.1)
составленный из этих чисел символ
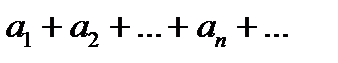 (15.2)
(15.2)
называется числовым рядом, а сами числа (15.1)называются членами ряда.
Вместо (15.2) ползуются знаком суммы, часто пишут так:
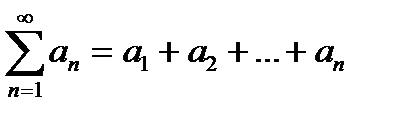
Выражение для n-го члена ряда при произвольнои n-называется общим членом ряда.
Станем последовательно складывать члены ряда, составляя суммы
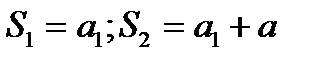

их называют частными суммами (или отрезками) ряда.
Определение 15.1: Сумма конечнего числа n первых членов ряда называется n-й частичной суммой ряда
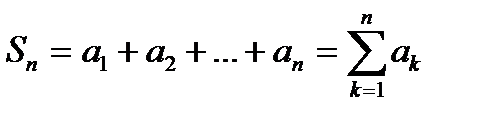 (15.3)
(15.3)
Рассмотрим последовательность, составленную из частичних сумм:
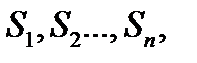

Таким образом, ставится вопрос: существует ли предел последовательности { 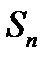 } при
} при 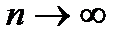 то есть:
то есть:
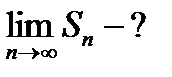
Определение15.2. Конечный или бесконечный предел S частичной суммы ряда (15.2) при 
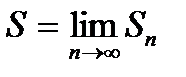
называется суммой ряда и пишется:
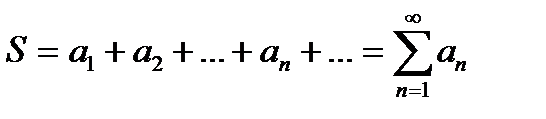
Если существует конечный предел:

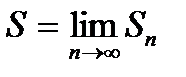
то говорят, что ряд сходится.
Если

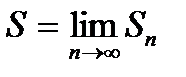
не существует или равен бесконечности, то говорят, что ряд (15.2) расходятся.
Пример 15.1. Найти S, 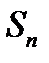 и
и 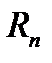 ряда
ряда
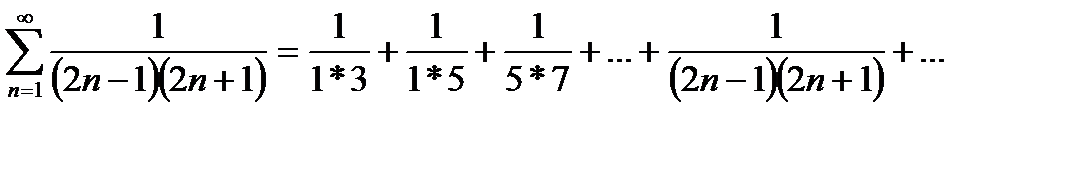 Решение: Имеем
Решение: Имеем 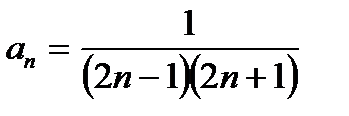
Записываем разложение дроби на простейшие с неорпеделенными коэффициентами:
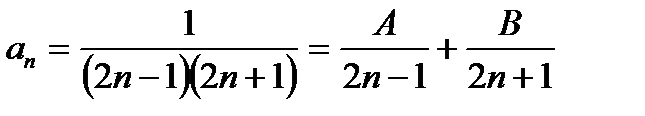
Полученное равенство умножаем на знаменатель дроби и получаем тождество:
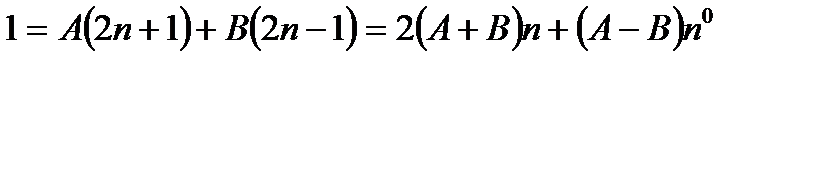
Сравнением коэффициентов при одинаковых степенях n, получаем систему уравнений:
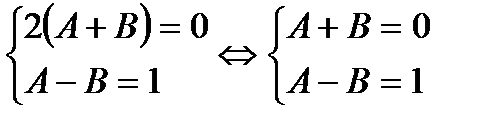
Из которых находим 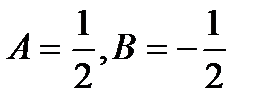
Таким образом 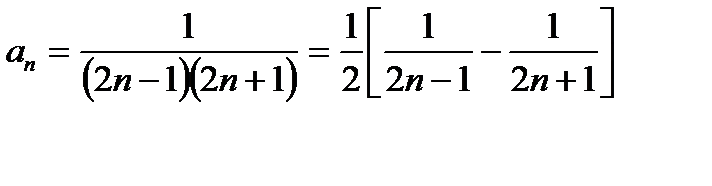
Представляя теперь каждый член ряда в виде суммы двух слагаемых, мы получаем следующее выражение для n-й частичной суммы:
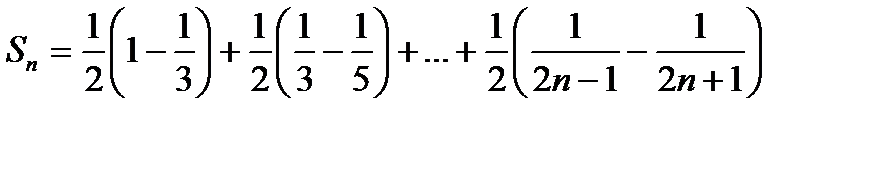 Очевидно, что в этой сумме все слагаемое попарно уничтожаются, кроме первого и последного, поэтому
Очевидно, что в этой сумме все слагаемое попарно уничтожаются, кроме первого и последного, поэтому

Откуда: 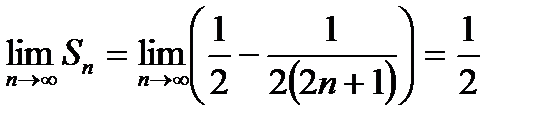
Следовательно, данный ряд сходится и его сумма 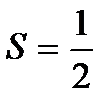
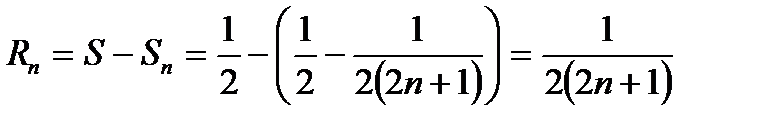

 2015-03-07
2015-03-07 1954
1954








