Для того чтобы ряд 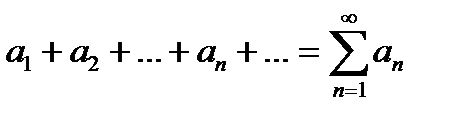
был сходящимся, необходимо и достаточно, чтобы при любом 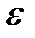 >0 можно было найти такое N, что при n>N и любом целом p>0 выполняется неравенство
>0 можно было найти такое N, что при n>N и любом целом p>0 выполняется неравенство 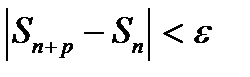
Или иначе
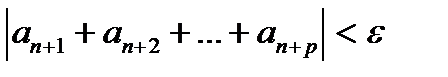
Так как: 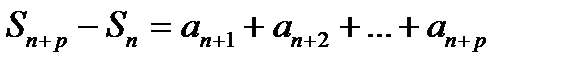
Доказательство этой теоремы очевидно: она просто утверждает, что для того, чтобы ряд сходился, необходимо и лостаточно, чтобы последовательность его частных сумм была фундаментальной, то есть сходилась. А это и есть определение сходимости ряда.
Рассмотрим ряд:
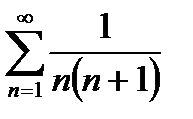 и докажем что он сходится. Для этого заметим, что:
и докажем что он сходится. Для этого заметим, что:

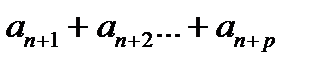 =
= 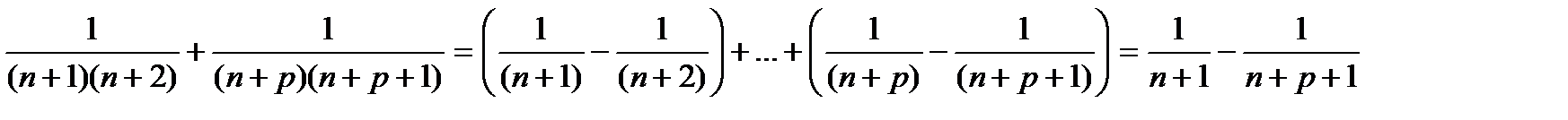 <
<  <
< 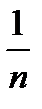 ,
,
А поэтому, взяв для 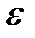 >0 число N такое, что
>0 число N такое, что
 >
> 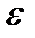 , будет для n>N иметь
, будет для n>N иметь 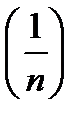 <
< 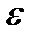 и
и
a 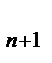 +a
+a 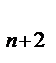 +…+a
+…+a 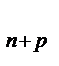 <
< 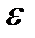
 2015-03-07
2015-03-07 322
322








