Доказательство второй части теоремы

Пусть выполнено условие (16.4) и q<1. рассмотрим число l, удовлетворяющее неравенству q< l <1.

Из определения предела и соотношения (16.4) следует, что 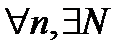, то есть 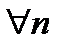, начиная с некоторого номера 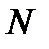, то есть 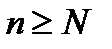будет иметь место неравенство

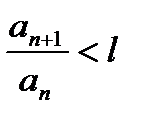(16.6)

Действительно, так как величина 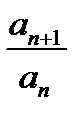стремится к пределу q, то разность 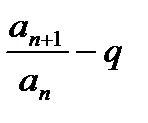может быть сколько угодно малым.

Тогда для любого 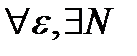как только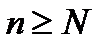

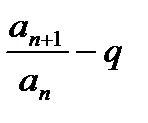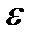
< < q+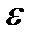

Так как 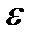достаточно мало, то 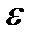и q выбираем так, чтобы q+ 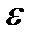<1, при 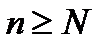, то есть

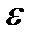< q+ <1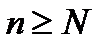

Отсюда получим

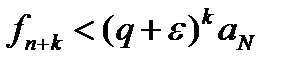
Для удобства обозначим q+ 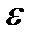= q₁, тогда

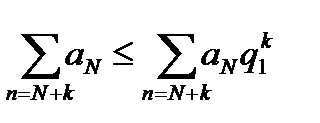
Геометрический ряд сходится, то и сходится ряд (16.1).

Пусть q>1. тогда из свойства (16.4) вытекает что

> l, ( )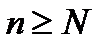

При достаточно большом N и тогда в силу свойства (16.3) ряд 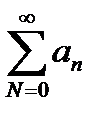расходится, а вместе с ним расходится и ряд (16.1).