Биномиальный ряд

Разложим в ряд Маклорена функцию

ƒ (x)= ,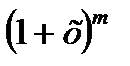

где m- произвольное постоянное число.

Заметим, что функция ƒ(х) является решением дифференциального уравнения:

(1+х)ƒ’(х)=mƒ(х) (21.1)

и удовлетворяет условию

ƒ (0)=1.

Действительно

ƒ’(х)=m .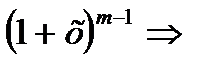

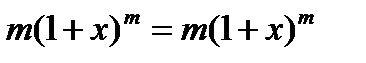Найдем степенной ряд, сумма которого S(x) удовлетворяет уравнению (21.1) и условию S(0)=1.

Пусть

S(x)= 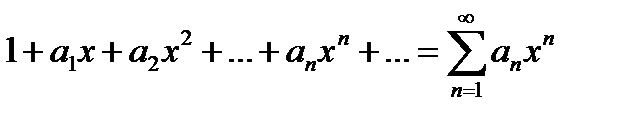(21.2)

Подставляя в уравнение (21.1), получим:

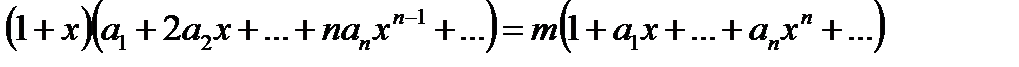
или

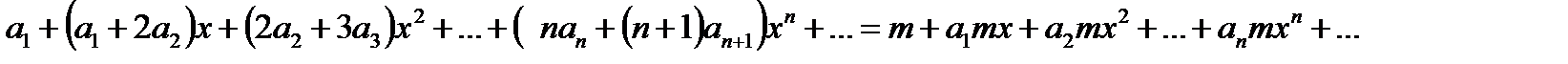
Приравнивая коэффициенты при одинаковых степенях х в разных частях равенства, находим:

, … ,

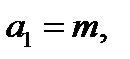
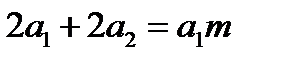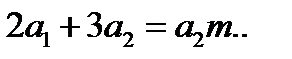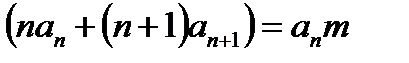Откуда для коэффициентов ряда получаем выражение

, , ,

.

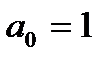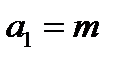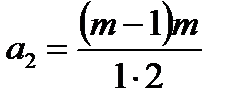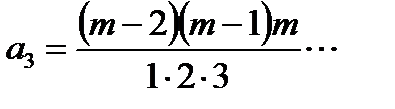
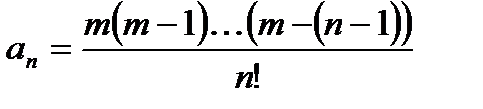Это биномиальные коэффициенты ряда. Подставляя их в формулу (21.2), получим:

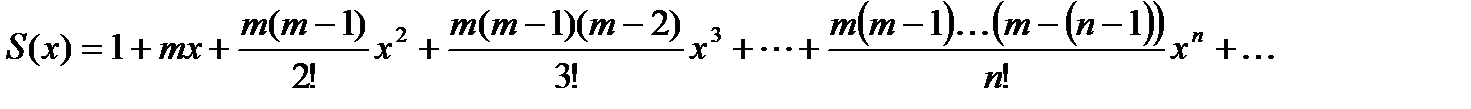(21.3)

Если m-целое число, то начиная с члена, содержащего 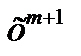, все коэффициенты равны нулю и ряд превращается в многочлен. При m- дробном отрицательном получаем бесконечный ряд.

Определим радиус сходимости ряда(21.3)

,

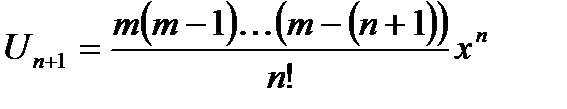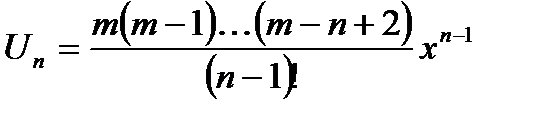
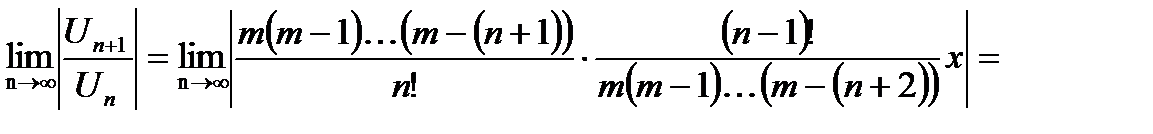
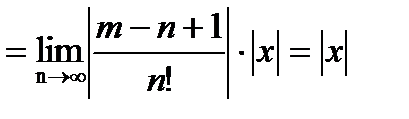
Таким образом, ряд (21.3) сходится при 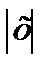<1.

В интервале (-1,1) ряд (21.3) представляет функцию S(x), удовлетворяющую дифференциальному уравнению (21.1) и условию S(0)=1. Так как дифференциальное уравнение (21.1) и условие S(0)=1 удовлетворяет единственная функция, то.. Следовательно, сумма ряда (21.3) тождественно равна функции 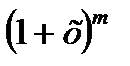, и мы получаем разложение 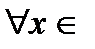(-1,+1):

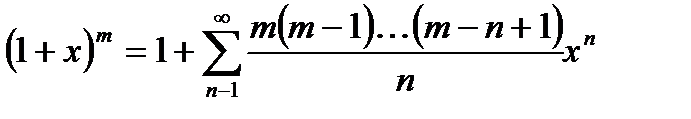
где 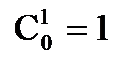, 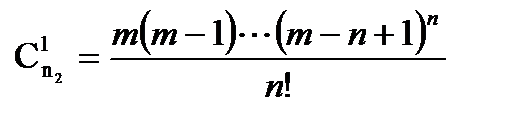(21.4)

В частности, при m=-1:

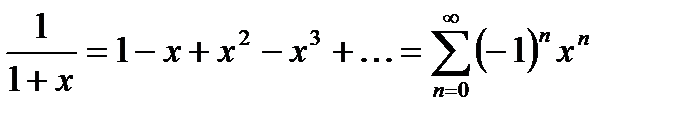
При m= 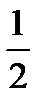, получаем

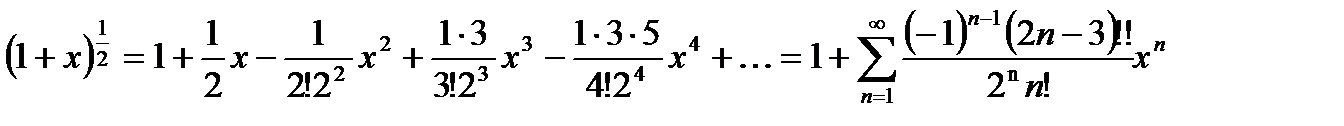(21.5)

При m= - 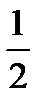, получаем

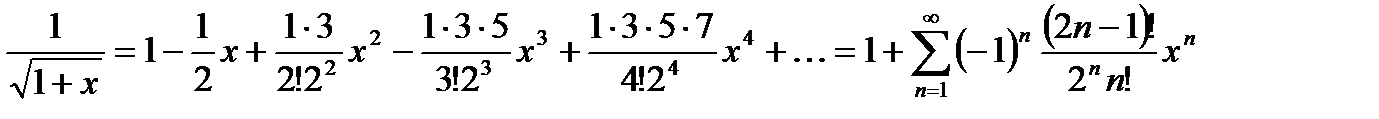(21.6)