Основные виды математических моделей

В зависимости от конкретной реализации проекта и его аппаратурного оформления, всё многообразие технологических процессов пищевой и химической промышленности можно разделить на четыре класса, исходя из временного и пространственного признаков:

- процессы, переменные во времени (нестационарные);

- процессы, не меняющиеся во времени (стационарные);

- процессы, в ходе которых их параметры изменяются в пространстве;

- процессы без пространственного изменения параметров.

Соответственно этому делению и математические модели, отражающие эти процессы, можно классифицировать следующим образом:

1) модели, неизменные во времени – статические модели;

2) модели, переменные во времени – динамические модели;

3) модели, неизменные в пространстве – модели с сосредоточенными параметрами;

4) модели, изменяющиеся в пространстве – модели с распределенными параметрами.

Рассмотрим модели с сосредоточенными параметрами.

Для данного класса моделей характерно постоянство переменных в пространстве. Математическое описание включает в себя алгебраические уравнения либо дифференциального уравнения первого порядка для нестационарных процессов. Примером объекта, описываемого данным классом моделей, является аппарат с идеальным (полным) перемешиванием потока. Скорость мешалки такова, что концентрация во всех точках аппарата одинакова [22].

Если на вход аппарата подано ступенчатое воздействие, то есть скачкообразное изменение концентрации в момент времени t=0 от 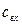до 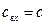- зависимость 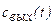примет вид (рис. 1.9а):

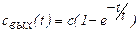, (1.17)

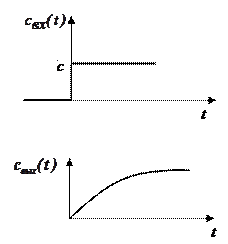где с - значение концентрации в момент времени t; 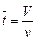- среднее время пребывания частиц потока в аппарате.

а)

б)

Рис. 1.9 - Зависимость 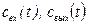при ступенчатом воздействии

Если на вход аппарата подано импульсное воздействие (метод вымывания), т.е. резко подали индикатор на вход аппарата с начальной концентрацией 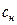и резко убрали подачу, то зависимость 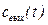примет вид: 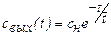(рис. 1.10).

Передаточная функция аппарата идеального смешения (апериодическое звено первого порядка) имеет вид:

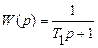, (1.18)

где 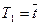- постоянная времени объекта, с.

Моделью идеального смешения описываются процессы, происходящие в цилиндрических аппаратах со сферическим дном в условиях больших скоростей перемещения и при наличии отражающих перегородок [18].

Рис. 1.10 - Зависимость 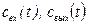при импульсном воздействии.

Модели с распределенными параметрами характеризуются тем, что переменные процесса могут изменяться как во времени, так и в пространстве, а также могут изменяться только в пространстве. Их математическое описание включает обычно дифференциальные уравнения в частных производных, либо обыкновенные дифференциальные уравнения в случае стационарных процессов с одной пространственной переменной. Примером процесса, описываемого такими моделями, служит трубчатый аппарат с большим отношением длины к диаметру (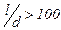) и значительной скоростью движения реагентов (рис. 1.11).

Модель идеального смешения соответствует аппарату, в котором поступающее в него вещество мгновенно распределяется по всему объему аппарата (рис. 1.12). Концентрация вещества в любой точке аппарата равна концентрации вещества на выходе из него.

Рис. 1.11 – Схема трубчатого аппарата

Зависимость концентрации вещества в потоке жидкости на входе в аппарате идеального смешения 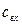и выходе из него 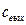имеет вид:

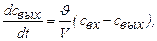(1.19)

где 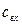- концентрация вещества на входе; 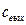-концентрация вещества на выходе; V - объем аппарата; 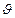- объемный расход потока через аппарат.

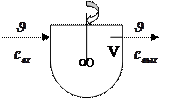Рис.1.12 - Аппарат идеального смешения

Стационарное состояние является основным рабочим режимом непрерывных технологических процессов.

Речь может идти о стационарных состояниях или режимах функционирования какой-либо системы, которая в каждый момент под действием внешних воздействий может выйти из этого состояния.

Существует два класса исследования стационарных состояний:

1. Задача анализа – определение неизвестных режимных переменных системы, при которых достигается заданное стационарное состояние;

2. Задача оптимального синтеза – выбор оптимального стационарного состояния среди множества возможных.

Таким образом, видим, что первая задача – это составная часть второй. Решением первой задачи является конечный набор числовых значений.

Основа моделей стационарных режимов – уравнение материального и энергетического баланса в системе. Всегда входной поток материи равен выходному потоку, накопления не происходит [7].

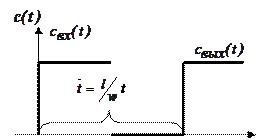Если на входе ступенчатый входной сигнал, то выходной сигнал повторяет входной со сдвигом (запаздыванием) по времени на величину среднего времени пребывание в аппарате (рис. 1.13):

		t
	0

Рис. 1.13 - Зависимость 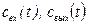при ступенчатом воздействии.

В случае импульсного входного сигнала функция отклика представлена на рис. 1.14.

Передаточная функция для аппарата идеального вытеснения имеет вид:

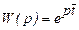, (1.20)

где 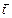- время транспортного запаздывания, это – звено чистого запаздывания.

Еще раз отметим, что модели идеального вытеснения соответствуют процессы, протекающие в трубчатых аппаратах при большом отношении длины трубы к диаметру.

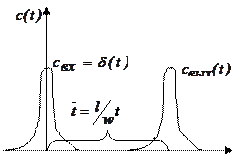Рис. 1.14 - Зависимость 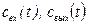при ступенчатом воздействии

К статическим относят модели инвариантные относительно времени. Они служат для описания процессов и явлений, независящих от времени. Соответствующее математическое описание в статических моделях не включает время как переменную и состоит из алгебраических уравнений, либо дифференциальных уравнений, в случае объектов с распределенными параметрами. Примером объекта, описываемого статической моделью, служит аппарат полного смешения объемом V в установившемся режиме работы, в который непрерывно подаются реагенты А и В в количестве 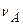и 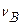и отводится продукт реакции Р. Причем 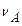+ 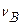= 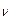( 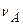и 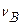- объемные расходы реагентов А и В соответственно)

Для математического описания аппарата применим уравнения материального баланса:

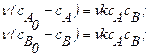(1.21)

где k – константа скорости реакции.

Динамические модели отображают изменение объекта во времени. Математическое описание таких объектов включает производную по времени. Часто динамическую модель объекта строят в виде передаточных функций.

Рассмотрим модель идеального вытеснения, в основе такой модели лежит допущение о поршневом течении без перемешивания вдоль потока при равномерном распределении вещества в направлении, перпендикулярном движению (рис. 1.15). Время пребывания всех частиц в системе одинаково и равно отношению объема системы к объемному расходу жидкости.

Такой поток, например, имеет место в трубчатом аппарате при турбулентном режиме течения жидкости через него [7].

Математическое описание модели идеального вытеснения имеет вид:

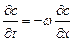, (1.22)

где t – время, с; х – координата, вдоль которой перемещается вещество; ω - линейная скорость перемещения вещества (потока), м/с.

Рис. 1.15 – Схема к модели идеального вытеснения

Для решения дифференциального уравнения в частных производных примем начальное условие: в начальный момент времени по всей длине аппарата начальная концентрация была равна некоторому значению 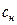, то есть:

с(0,х)=с_н(х), при t=0, 0<x≤l. (1.23)

Примем граничное условие: в аппарате в любой момент времени входная концентрация есть некоторая функция от времени, т.е.:

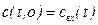, при х=0, t>0. (1.24)

Тогда решение уравнения (1.22) имеет вид:

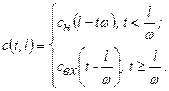(1.25)

Из решения (1.25) следует, что любое изменение концентрации на входе в аппарате идеального вытеснения появляется на его выходе через время, равное среднем времени пребывания 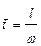, где l - длина аппарата.

Рассмотрим два основных входных сигнала: ступенчатый и импульсный.

Примером динамической модели может служить модель рассмотренного выше аппарата полного смещения, но работающего в неустановившемся режиме. В этом случае математическое описание аппарата включат в следующие уравнения материального баланса:

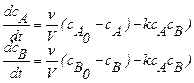(1.26)

А так же начальные условия 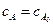, , 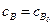при t=0.

Типовыми моделями структуры потоков в технологических аппаратах являются модель идеального смешения и модель идеального вытеснения.

Рассмотрим однопараметрическую диффузионную модель (рис. 1.16).

За основу возьмем модель идеального вытеснения (1.22), но при наличии обратного перемешивания, подчиняющегося формальному закону диффузии [3].

В качестве параметра модели служит коэффициент турбулентной диффузии (коэффициент продольного перемешивания) 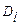(м²/с), который определяется опытным путем.

При составлении модели приняты следующие допущения: изменение концентрации вещества является непрерывной функцией координаты; концентрация вещества в данном сечении постоянна; объемная скорость потока и коэффициент продольного перемешивания не изменяются по длине и сечению потока.

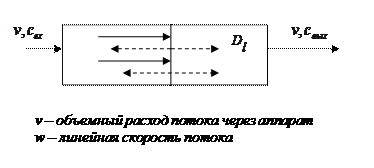
Рис. 1.16 – Схема к диффузионной модели

При таких допущениях модель запишем, основываясь на законе сохранения массы:

накопление = приход вещества - расход вещества

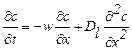(1.27)

Уравнение (1.25) является основным уравнением диффузионной модели.

Начальное условие: 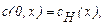при t=0 – профиль концентрации в начальный момент времени определен и равен .

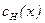Граничные условия задаются из условия материального баланса на концах аппарата. Рассмотрим схемы потоков у левого и правого края аппарата (рис. 1.17 а,б).

Общее правило: сумма потоков вещества, походящих к границе должна быть равна сумме потоков вещества отходящего от границы, тогда получаем:

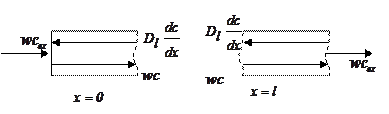
а) б)

Рис. 1.17 – Схемы потоков у левого и правого края аппарата

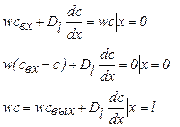(1.26)

Для первого края обычно принимают 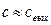, тогда получаем, что:

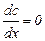. (1.27)

Такие условия называются - граничные условия по Данквертсу.

В случае, когда на входе диффузионной модели ступенчатая функция, график представлен на рис. 1.18.

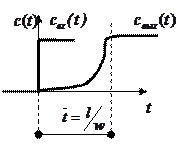
Рис. 1.18 – График функции отклика при ступенчатой входной функции

Для случая импульсной функции на входе аппарата функция отклика представлена на рисунке 1.19.

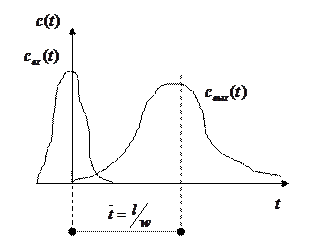
Рис. 1.19 – График функции отклика при импульсной входной функции

Передаточная функция достаточно сложная, она не выражает ни одним из типовых звеньев.

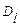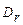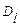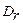Рассмотрим двухпараметрическую диффузионную модель. В этой модели учитывается перемешивание потока в продольном и радиальном направлениях (рис. 1.18). Таким образом, двухпараметрическая модель характеризуется двумя параметрами: коэффициентом продольного и радиального перемешивания. При этом принимается, что величины и не изменяются по длине и сечению аппарата, а линейная скорость w=v/s постоянна, где v- объемный расход потока через аппарат, м³/ч.

.

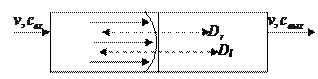
Рис. 1.20 – Схема движения потоков к двухпараметрической диффузионной модели

Для случая одномерного движения потока в аппарате цилиндрической формы с постоянной по длине и сечению скоростью ω уравнение двухпараметрической диффузионной модели имеет вид [5, 6]:

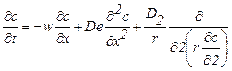. (1.28)

Начальное условие: с(o,x,r)=0 при t=0.

Граничные условия:

- исходя из геометрии для центра аппарата: r=0, c(t,0,0)=с₀δ(0) при х=0;

- для слоёв возле стенок аппарата: 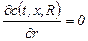при r=R;

- для левого края аппарата: 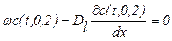при х=0;

для правого края аппарата: 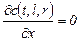при x=l.

При опытном определении величин коэффициентов продольного D_l и радиального D₂ перемешивания их обычно представляют в виде безразмерных критериев Пекле: 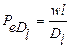и .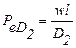

Двухпараметрическая диффузионная модель используется для описания движения потоков в аппаратах колонного типа с небольшим отношением длины к диаметру, и большой поперечной неравномерностью скоростей потоков. Ввиду сложности решения такая модель используется значительно реже однопараметрической [8].

Рассмотрим ячеечную модель. Впервые рассматриваемая модель была предложена для каскада реакторов с мешалками. В этом случае аппарат состоит из ряда последовательно соединенных ячеек, через которые проходит поток вещества: v-расход вещества через аппарат, причём для простоты примем, что .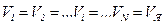

…

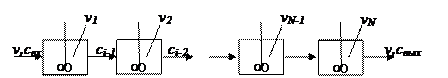
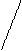
Рис. 1.21 – Схема ячеечной модели

Примем следующие допущения:

1) в каждой ячейке осуществляется идеальное перемешивание;

2) между ячейками отсутствует обратное перемешивание.

Параметрами ячеечной модели, количественно характеризующими продольное перемешивание, служит число ячеек полного перемешивания N. С увеличением N структура потока приближается к модели полного вытеснения, а с уменьшением N - к модели идеального смещения.

Запишем уравнение сохранения массы для каждой из ячеек:

;

;

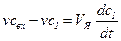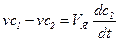…………………… (1.29)

;

………………………

.

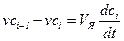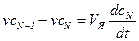Разделим левые и правые части (1.29) на v:

;

;

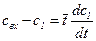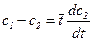………………… (1.30)

;

………………………

;

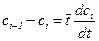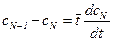где 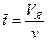– среднее время пребывания частиц потока в каждой ячейке.

Соответствующие начальные условия имеют вид: 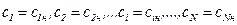, при t=0.

Cистема из N линейных дифференциальных уравнений в обыкновенных производных (1.30) вместе с начальными условиями образуют ячеечную модель структуры потока.

Рассмотрим отклики ячеечной модели на два стандартных возмущения (таблица 1.4).

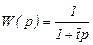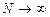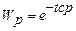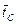Если рассматривать передаточные функции объектов, описываемых ячеечной моделью, то тогда число ячеек N=1, то передаточная функция имеет вид , что соответствует передаточной функции модели идеального смешения в модель их смещения. Когда число ячеек , то передаточная функция , где - среднее время пребывания в объекте описываемая ячеечной моделью – звено чистого запаздывания соответственной модели идеального вытеснения.

Данная модель применяется при описании процессов, происходящих в группе последовательно соединенных аппаратов с мешалками, а так же для описания процессов массообмена в обсорбционных и экстракционных колоннах.

Таблица 1.4

1. Ступенчатое возмущение со скачкообразным уменьшением концентрации до 0 (метод вымывания) 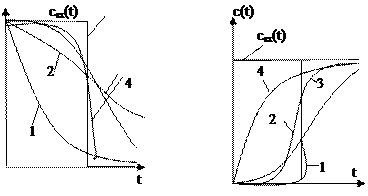c(t) 1-идеальное смещение при числе ячеек n2, n3, n4, причём n2 < n3<n4 5-идеальное вытеснение

2. Импульное возмущение

3. Ступенчатое возмущение со скачкообразным возрастанием концентрации рационально 1,2,3-идеальное вытеснение при числе ячеек n2 и n3, n2 < n3 4- идеальное смещение