Раздел 2. Основы математического анализа.
Тема 2.6 Определенный интеграл.
Основные понятия.
Пусть функция
y=f(x) непрерывна на отрезке
[ a;b ]. Разделим отрезок
[ a;b ] на
n произвольных частей точками
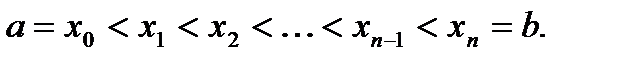
Выберем на каждом элементарном отрезке
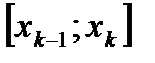
произвольную точку
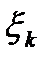
(кси) и найдем длину каждого такого отрезка
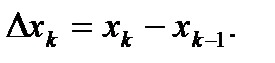
Определение. Интегральной суммой для функции y=f(x) на отрезке [ a;b ] называется сумма вида:
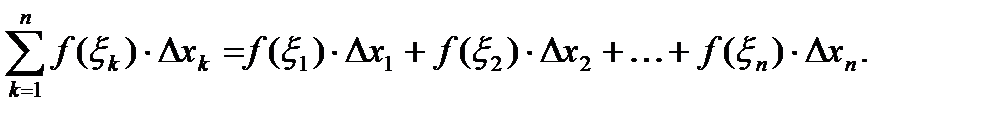
Определение. Определенным интегралом от функции y=f(x) на отрезке [ a;b ] (или впределах от а до b) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
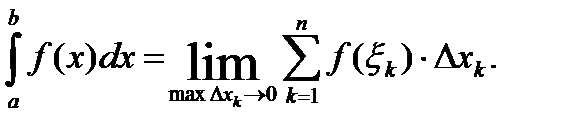
Концы a,b отрезка (промежутка интегрирования) называются пределами интегрирования (a – нижний; b – верхний).
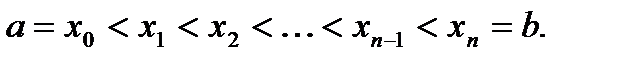 Выберем на каждом элементарном отрезке
Выберем на каждом элементарном отрезке 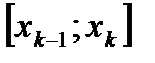 произвольную точку
произвольную точку 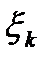 (кси) и найдем длину каждого такого отрезка
(кси) и найдем длину каждого такого отрезка 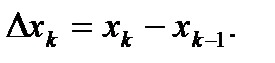
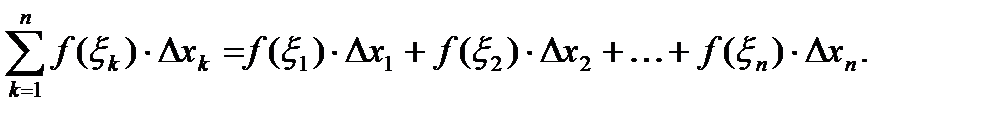
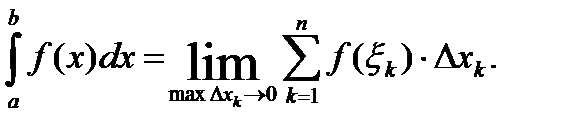
 2015-03-07
2015-03-07 581
581







