Свойство 1. Определенный интеграл от непрерывной функции не зависит от выбора первообразной для подынтегральной функции, т.к. определенный интеграл от суммы является числом.
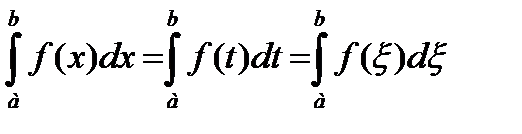
Следствие. 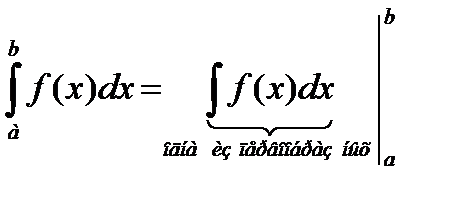 .
.
Данное соотношение устанавливает связь между определенным и соответствующим неопределенным интегралом.
Формальная разница между определенным и неопределенным интегралом в том, что определенный интеграл – число, а неопределенный интеграл – функция.
Свойство 2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
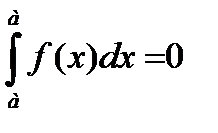 .
.
Свойство 3. При перестановке пределов интегрирования определенный интеграл меняет свой знак: 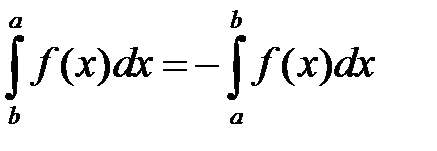 .
.
Свойство 4. Постоянный множитель можно выносить за знак определенного интеграла:
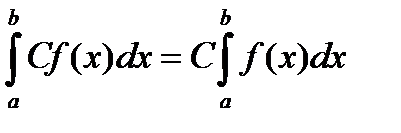 .
.
Свойство 5. Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций. 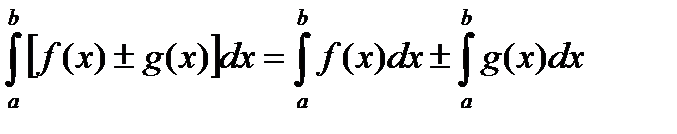 .
.
Свойство 6. Если взять точку с, лежащую внутри отрезка [ a;b ], то
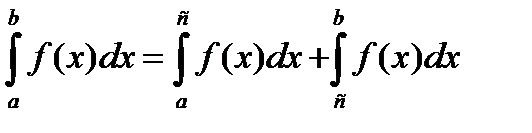
Свойство 7. Если 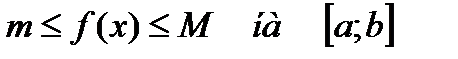 ,то
,то
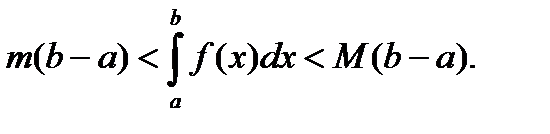
| a |
| с |
| b |
| y |
| x |
| A |
| B |
| C |
| D |
| E |
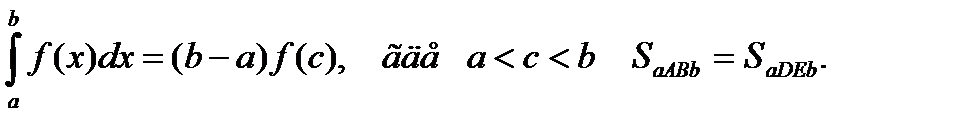
 2015-03-07
2015-03-07 1025
1025
