2015-03-27
1682
Цель: рассмотреть методы смягчения или устранения проблем гетероскедастичности и научиться применять их на практике при решении задач эконометрики.
Ключевые слова: вес, гетероскедастичность, гомоскедастичность.
План лекции:
1. Способы смягчения гетероскедастичности.
1.Способы смягчения гетероскедастичности.
Для устранения гетероскедастичности нужно найти способ придать наибольший вес наблюдению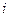 
, у которого среднее квадратическое отклонение случайной составляющей 
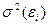максимально (такие наблюдения обладают самым низким качеством); и малый вес наблюдению, у которого среднее квадратическое отклонение случайной составляющей 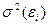минимально (такие наблюдения обладают самым высоким качеством). Тогда мы получим более точные (эффективные) оценки параметров уравнения регрессии: 
.
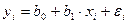Разделим правую и левую части уравнения на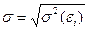 
. Получим:
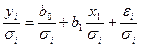
Введем новые переменные:
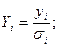
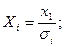
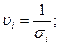
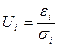
Тогда уравнение регрессии примет вид:
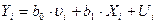
Преобразованное уравнение относится к двухфакторному уравнению регрессии (1-й фактор -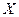 
, 2-й фактор - 
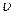). Данное уравнение представляет собой так называемую взвешенную регрессию (с весами 
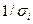). При этом наблюдениям высокого качествами с меньшими 
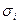придаются большие веса 
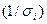и наоборот. Случайная составляющая в 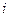-м наблюдении 
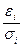имеет постоянную дисперсию, т.е. модель будет гомоскедастичной.
|
|
|
Данный способ устранения гетероскедастичности применим, если известны фактические значения 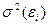, что редко встречается на практике.
Однако, если мы сможем подобрать некоторую величину, пропорциональную 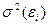в каждом наблюдении 
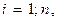и разделим на нее обе части уравнения, то гетероскедастичность будет устранена.
Например, может оказаться целесообразным предположить, что дисперсии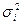 
пропорциональны 
.
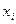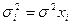
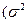- коэффициент пропорциональности).
Тогда уравнение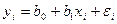 
преобразуется делением его левой и правой частей на 
:
.
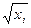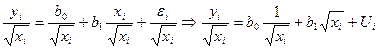Несложно показать, что для случайных отклонений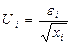 
выполняется условие гомоскедастичности. Следовательно, для регрессии применим обычный МНК. Действительно, в силу выполнимости предпосылки 
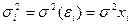имеем:
.
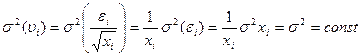Таким образом, оценив по МНК коэффициенты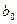 
и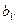 
, затем возвращаются к исходному уравнению регрессии .
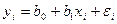В случае, если зависимость 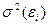от 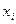целесообразнее выразить квадратичной функцией, т.е. предположить, что дисперсии 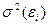отклонений пропорциональны значениям 
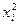, то соответствующим преобразованием будет деление уравнения регрессии на :
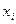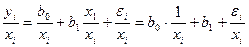
Дисперсия случайной составляющей в этом уравнении может быть записана как
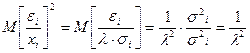
То есть она будет постоянна для всех наблюдений. Следовательно, гетероскедастичность в преобразованном уравнении регрессии отсутствует.
|
|
|
После определения по МНК оценок коэффициентов b0 и b1 для уравнения регрессии возвращаются к исходному уравнению.
