1. Площадь плоской фигуры
а) Площадь криволинейной трапеции, ограниченной кривой 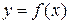 , прямыми
, прямыми 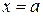 и
и 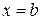 и отрезком
и отрезком 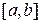 , вычисляется по формуле
, вычисляется по формуле 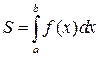 .
.
б) Площадь фигуры, ограниченной кривыми 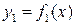 и
и 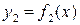
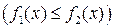 и прямыми
и прямыми 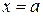 и
и 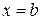 , находится по формуле
, находится по формуле 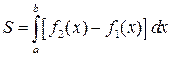 .
.
в) Если кривая задана параметрическими уравнениями 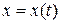 и
и 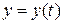 , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми 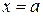 и
и 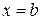 и отрезком
и отрезком 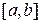 , выражается формулой
, выражается формулой 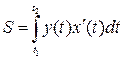 , где t 1 и t 2 определяются из уравнений
, где t 1 и t 2 определяются из уравнений 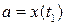 и
и 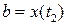 .
.
г) Площадь криволинейного сектора находится по формуле 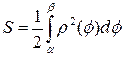 .
.
2. Длина дуги плоской кривой
а) Если кривая 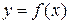 на отрезке
на отрезке 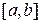 – гладкая, то есть
– гладкая, то есть 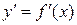 – непрерывна, то длина соответствующей дуги этой кривой находится по формуле
– непрерывна, то длина соответствующей дуги этой кривой находится по формуле 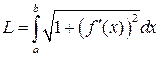
б) Если уравнение кривой задано параметрически, то длина дуги кривой, соответствующая монотонному изменению параметра t от t 1 до t 2, вычисляется по формуле 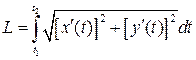
в) Если кривая задана в полярных координатах, то
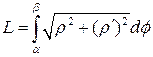
3. Объем тела
а) Если площадь сечения тела плоскостью, перпендикулярной оси Ох может быть выражена как функция от x, то есть в виде 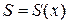 , то объем части тела, заключенной между перпендикулярными оси Ох плоскостями
, то объем части тела, заключенной между перпендикулярными оси Ох плоскостями 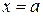 и
и 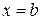 , находится по формуле:
, находится по формуле:
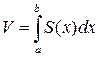
б) Если криволинейная трапеция, ограниченная кривой 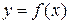 и прямыми
и прямыми 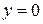 ,
, 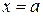 и
и 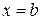 , вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле:
, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле:
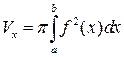
в) Если фигура, ограниченная кривыми 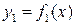 и
и 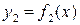 и прямыми
и прямыми 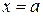 и
и 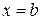 , вращается вокруг оси Ох, то объем тела вращения:
, вращается вокруг оси Ох, то объем тела вращения:
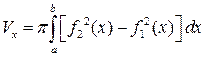
4. Площадь поверхности тела вращения
а) Если дуга гладкой кривой 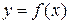 вращается вокруг оси Ох, то площадь поверхности вращения вычисляется по формуле:
вращается вокруг оси Ох, то площадь поверхности вращения вычисляется по формуле:
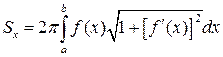
б) Если кривая задана параметрическими уравнениями 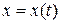 и
и 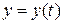 , то
, то
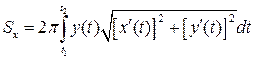
 2015-03-07
2015-03-07 353
353








