Кафедра Теории функций и функционального анализа
Кафедра Геометрии и высшей алгебры
Водахова В.А., Тлупова Р.Г.,
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАЧИ
ДЛЯ СТУДЕНТОВ ФАКУЛЬТЕТА ИНФОРМАТИКИ И УПРАВЛЕНИЯ
Нальчик 2015.
УДК 51(076.1)
ББК 22.171.27
В-62
Водахова В.А., Тлупова Р.Г. – ТЕОРИЯ ВЕРОЯТНОСТЕЙ. Методические указания и задачи для студентов факультета информатики и управления.– Нальчик – 2015 - 75 стр.
Методические указания и задачи по курсу теории вероятностей охватывают все основные разделы курса теории вероятностей,читаемого в КБГУ.
В целях стимулирования самостоятельной работы студентов в начале каждой главы приводятся решения типовых примеров, предназначенных для усвоения основных теоретических положений, поясняются необходимые предпосылки применения вероятностных методов.
Для удобства работы приводятся специально подобранный по каждой теме перечень задач. Все задачи снабжены ответами.
Задачник предназначен для студентов всех специальностей факультета информатики и управления. Однако он может быть рекомендован и всем желающим самостоятельно изучать курс теории вероятностей.
Рецензент: к.ф.-м.н., доцент –
Рекомендовано РИС университета.
Кабардино – Балкарский
государственный университет, 2015
 ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используются при непосредственном вычислении вероятностей.
Множества, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Число всевозможных перестановок из n элементов обозначают Pn это число равно п! (энфактариал):
Pn = п!, (1.1)
где
п!=1×2×3×…×п. (1.2)
Размещениями называют множества, составленные из п различных элементов по т элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений определяется формулой
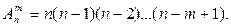 (1.3)
(1.3)
Сочетаниями из n различных элементов по т элементов из числа п заданных называются, и которые отличаются хотя бы одним элементом. Число сочетаний п элементов по т обозначают 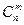 или
или 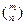 . Это число выражается формулой
. Это число выражается формулой
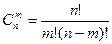 . (1.4)
. (1.4)
Замечание 1. По определению полагают 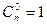 .
.
Для числа сочетаний справедливы равенства:
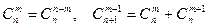 , (1.5)
, (1.5)
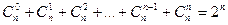 . (1.6)
. (1.6)
Последнее равенство иногда формулируется в виде следующей теоремы о конечных множествах:
Число всех подмножеств множества, состоящего из п элементов,
равно 2п.
Отметим, что числа перестановок, размещений и сочетаний связаны равенством 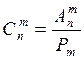 .
.
Замечание 2. Выше предполагалось, что все п элементов различны. Если же некоторые элементы повторяются, то в этом случае множества с повторениями вычисляют по другим формулам.
Например, если п элементов есть n1 элементов одного вида, n2 элемента другого вида и т.д., то число перестановок с повторениями определяется формулой
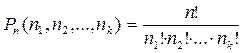 , (1.7)
, (1.7)
где n1 + n2 +…+ nk =п.
Число размещений по т элементов с повторениями из п элементов равно пт, то есть 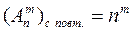 . (1.8)
. (1.8)
Число сочетаний с повторениями из п элементов по т элементов равно числу сочетаний без повторений из п+т-1 элементов т, то есть
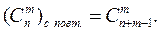 . (1.9)
. (1.9)
При решении задач комбинаторики используют следующие правила.
Правило суммы. Если некоторый объект А может быть выбран из множества объектов т способами, а другой объект В может быть выбран п способами, то выбрать либо А, либо В можно т+п способами.
Правило произведения. Если объект А можно выбрать из множества объектов т способами и после каждого такого выбора объект В можно выбрать п способами, то пара объектов (А, В) в указанном порядке может быть выбрана т × п способами.
Классическая схема подсчета вероятностей пригодна для решения ряда сугубо практических задач. Рассмотрим, например, некоторое множество элементов объекта N. Это могут быть изделия, каждое из которых является годным или бракованным, или детали, каждая из которых является стандартной или бракованной. Подобного рода ситуации описываются урновой схемой: в урне имеется N шаров, из них М окрашенных (меченных), оставшееся (N-М) не окрашенных (не меченных). Из урны, содержащей N шаров, в которой находится М окрашенных шаров, извлекается п шаров. Требуется определить вероятность, того, что при выборке объема п будет обнаружено т окрашенных шаров. Обозначим через А событие «в выборке объема п имеется т окрашенных шаров», тогда
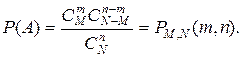 (1.10)
(1.10)
Пример 1. Сколькими различными способами можно выбрать три лица на три различные должности из десяти кандидатов?
Решение. Воспользуемся формулой (1.3). При п=10, т=3 получаем
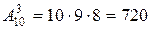 .
.
 2015-03-07
2015-03-07 841
841







