В задачах 5.1-5.10 найти производные следующих функций.
5.1 а) 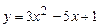 ; б)
; б) 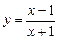 ; в)
; в) 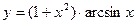 .
.
5.2 а) 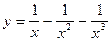 ; б)
; б) 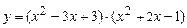 ;
;
в) 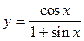 .
.
5.3 а) 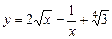 ; б)
; б) 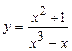 ; в)
; в) 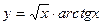 .
.
5.4 а) 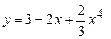 ; б)
; б) 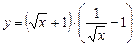 ;
;
в) 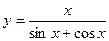 .
.
5.5 а) 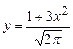 ; б)
; б) 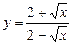 ; в)
; в) 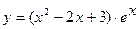 .
.
5.6 а) 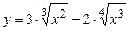 ; б)
; б) 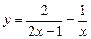 ; в)
; в) 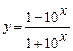 .
.
5.7 а) 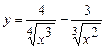 ; б)
; б) 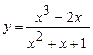 ; в)
; в) 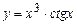 .
.
5.8 а) 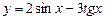 ; б)
; б) 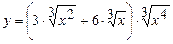 ;
;
в) 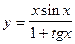 .
.
5.9 а) 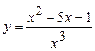 ; б)
; б) 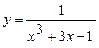 ;
;
в) 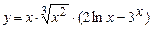 .
.
5.10 а) 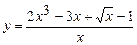 ; б)
; б) 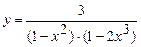 ;
;
в) 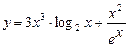 .
.
5.11 Показать, что функция 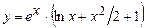 удовлетворяет условию:
удовлетворяет условию: 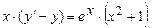
В задачах 5.12-5.21 найти производные следующих функций:
5.12 а) 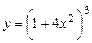 ; б)
; б) 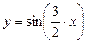 ; в)
; в) 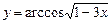 .
.
5.13 а) 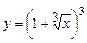 ; б)
; б) 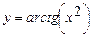 ; в)
; в) 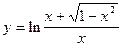 .
.
5.14 а) 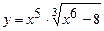 ; б)
; б) 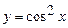 ; в)
; в) 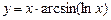 .
.
5.15 а) 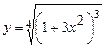 ; б)
; б) 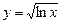 ; в)
; в) 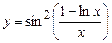 .
.
5.16 а) 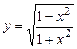 ; б)
; б) 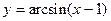 ; в)
; в) 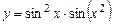 .
.
5.17 а) 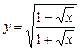 ; б)
; б) 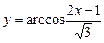 ; в)
; в) 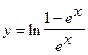 .
.
5.18 а) 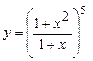 ; б)
; б) 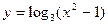 ; в)
; в) 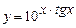 .
.
5.19 а) 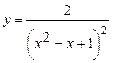 ; б)
; б) 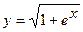 ; в)
; в) 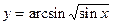 .
.
5.20 а) 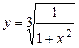 ; б)
; б) 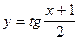 ; в)
; в) 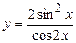 .
.
5.21 а) 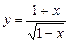 ; б)
; б) 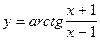 ; в)
; в) 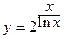 .
.
В задачах 5.22-5.49 найти производные следующих функций:
5.22 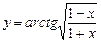 . 5.23
. 5.23 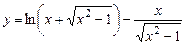 .
.
5.24 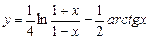 . 5.25
. 5.25 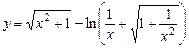 .
.
5.26 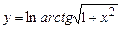 . 5.27
. 5.27 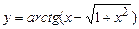 .
.
5.28 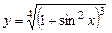 . 5.29
. 5.29 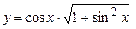 .
.
5.30 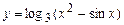 . 5.31
. 5.31 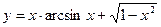 .
.
5.32 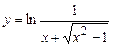 . 5.33
. 5.33 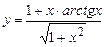 .
.
5.34 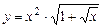 . 5.35
. 5.35 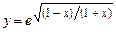 .
.
5.36 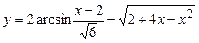 . 5.37
. 5.37 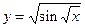 .
.
5.38 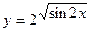 . 5.39
. 5.39 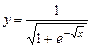 .
.
5.40 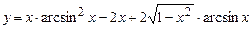 .
.
5.41 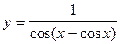 . 5.42
. 5.42 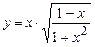 .
.
5.43 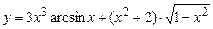 .
.
5.44 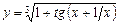 . 5.45
. 5.45 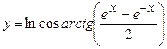 .
.
5.46 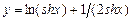 . 5.47
. 5.47 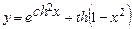 .
.
5.48 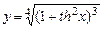 . 5.49
. 5.49 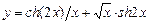 .
.
Логарифмической производной функции 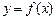 называется производная от логарифма этой функции, т.е.
называется производная от логарифма этой функции, т.е.  .
.
Применение предварительного логарифмирования функции приводит к следующему, часто более простому, способу вычисления её производной: 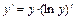 . Например, для степенно-показательной функции
. Например, для степенно-показательной функции 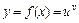 , где
, где 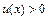 ,
, 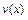 - дифференцируемые функции:
- дифференцируемые функции:
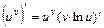 .
.
В задачах 5.50-5.59 найти производные функций, используя предварительное логарифмирование:
5.50 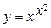 . 5.51
. 5.51 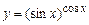 .
.
5.52 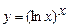 . 5.53
. 5.53 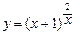 .
.
5.54 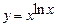 . 5.55
. 5.55 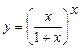 .
.
5.56 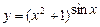 . 5.57
. 5.57 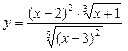 .
.
5.58 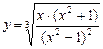 . 5.59
. 5.59 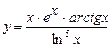 .
.
 2015-03-20
2015-03-20 585
585







