Производной 2-ого порядка от функции 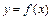 называется производная от её первой производной и обозначается
называется производная от её первой производной и обозначается 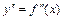 , т. е.
, т. е. 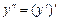 . В общем производной порядка
. В общем производной порядка 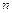 (
(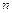 - ой производной) называется производная от
- ой производной) называется производная от 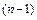 -ой производной и обозначается
-ой производной и обозначается 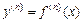 , т.е.
, т.е. 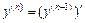 . Для производной
. Для производной 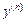 используется также обозначение
используется также обозначение 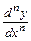 .
.
Производная 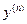 функции
функции 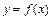 находится её последовательным дифференцированием:
находится её последовательным дифференцированием: 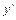 ,
, 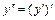 ,…,
,…, 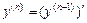 . Если функция
. Если функция 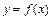 задана параметрически, то её производные высших порядков находятся по формулам:
задана параметрически, то её производные высших порядков находятся по формулам: 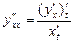 ,
, 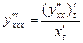 ,….
,….
В задачах 5.72-5.80 найти производные второго порядка от следующих функций:
5.72 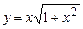 . 5.73
. 5.73 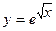 . 5.74
. 5.74 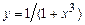 .
.
5.75 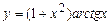 . 5.76
. 5.76 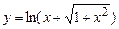 . 5.77
. 5.77 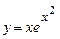 .
.
5.78 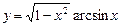 . 5.79
. 5.79 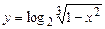 . 5.80
. 5.80 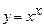 .
.
В задачах 5.81-5.84 найти производные указанного порядка от следующих функций:
5.81 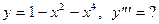 5.82
5.82 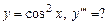
5.83 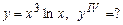 5.84
5.84 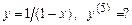
В задачах 5.85-5.90 найти формулу для 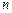 -ой производной от следующих функций:
-ой производной от следующих функций:
5.85 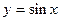 . 5.86.
. 5.86. 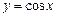 . 5.87
. 5.87 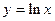 . 5.88
. 5.88 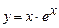 . 5.89
. 5.89 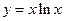 . 5.90
. 5.90 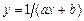 .
.
В задачах 5.91-5.96 найти производные 2-го порядка следующих функций, заданных параметрически:
5.91 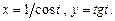 5.92
5.92 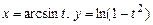 .
.
5.93 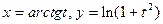 . 5.94
. 5.94 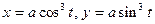 .
.
5.95 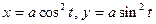 . 5.96
. 5.96 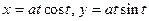 .
.
 2015-03-20
2015-03-20 342
342








