Если дифференцируемая функция 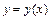 задана неявно уравнением
задана неявно уравнением 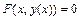 , то производная
, то производная 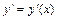 этой неявной функции может быть найдена из уравнения
этой неявной функции может быть найдена из уравнения 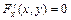 , линейного относительно
, линейного относительно 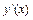 , где
, где 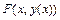 -рассматривается как сложная функция переменной
-рассматривается как сложная функция переменной 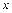 .
.
Если 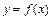 и
и 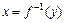 -взаимно обратные дифференцируемые функции и
-взаимно обратные дифференцируемые функции и 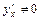 , то справедлива формула:
, то справедлива формула: 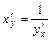 (правило дифференцирования обратной функции).
(правило дифференцирования обратной функции).
Если дифференцируемая функция 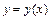 задана параметрически:
задана параметрически: 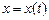 ,
, 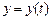
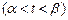 , где
, где 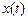 ,
, 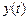 -дифференцируемые функции и
-дифференцируемые функции и  , то справедлива формула:
, то справедлива формула: 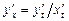 .
.
При дифференцировании сложных и обратных функций, а также функций заданных неявно и параметрически для производной используют обозначения типа 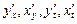 там, где необходимо уточнить, по какой переменной ведётся дифференцирование.
там, где необходимо уточнить, по какой переменной ведётся дифференцирование.
В задачах 5.60-5.64 для функций 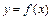 , заданных неявно, найти
, заданных неявно, найти 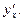
5.60 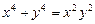 . 5.61
. 5.61  . 5.62
. 5.62 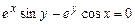 .
.
5.63 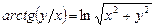 . 5.64
. 5.64 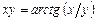 .
.
В задачах 5.65-5.71 для функций 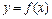 , заданных параметрически, найти
, заданных параметрически, найти 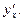
5.65 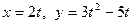 . 5.66
. 5.66 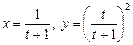 .
.
5.67 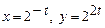 . 5.68
. 5.68 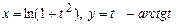 .
.
5.69 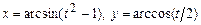 .
.
5.70 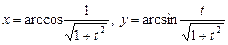
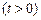 .
.
5.71 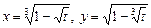 .
.
 2015-03-20
2015-03-20 1135
1135








