Если каждому значению действительной переменной 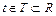 поставлен в соответствие вектор
поставлен в соответствие вектор 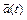 , то говорят, что на множестве
, то говорят, что на множестве 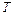 задана вектор-функция
задана вектор-функция 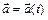 действительной переменной
действительной переменной 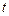 . Задание вектор-функции
. Задание вектор-функции 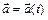 равносильно заданию трёх числовых функций
равносильно заданию трёх числовых функций 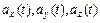 - координат вектора
- координат вектора 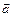 :
: 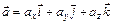 , или, кратко,
, или, кратко, 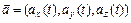 .
.
Если вектор 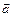 является радиус-вектором точки
является радиус-вектором точки 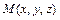 , то его обозначают
, то его обозначают  . Годографом вектор-функции
. Годографом вектор-функции 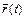 называется линия, описываемая в пространстве концом вектора
называется линия, описываемая в пространстве концом вектора 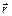 . Всякую линию в пространстве можно рассматривать как годограф некоторой вектор-функции
. Всякую линию в пространстве можно рассматривать как годограф некоторой вектор-функции 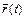 . Параметрические уравнения годографа:
. Параметрические уравнения годографа: 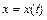 ,
, 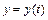 ,
, 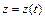 .
.
Производной вектор-функции 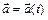 по аргументу
по аргументу 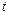 называется вектор-функция
называется вектор-функция 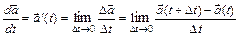 . Если
. Если 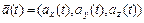 , то
, то 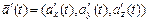 . Вектор-функция имеющая производную в данной точке, называется дифференцируемой в этой точке. Производная
. Вектор-функция имеющая производную в данной точке, называется дифференцируемой в этой точке. Производная 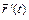 есть вектор, направленный по касательной к годографу вектор-функции
есть вектор, направленный по касательной к годографу вектор-функции 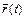 .
.
 2015-03-20
2015-03-20 1158
1158
