Задача потребительского выбора

Математическую модель задачи потребительского выбора в общем виде.

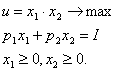
Составим функцию Лагранжа.

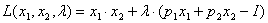
Найдем частные производные по каждой переменной.

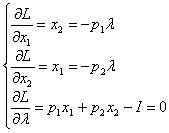
Разделим первое уравнение на второе.

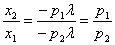
Следовательно .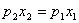

Подставим в третье уравнение системы.

.

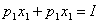Откуда , .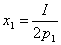

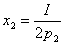1.Определение производственной функции и ее свойства.

Производственная функция – это зависимость между набором факторов производства и максимально возможным объемом продукта, производимым с помощью данного набора факторов.

Производственная функция всегда конкретна, т.е. предназначается для данной технологии. Новая технология – новая производительная функция. С помощью производственной функции определяется минимальное количество затрат, необходимых для производства данного объема продукта. Производственные функции, независимо от того, какой вид производства ими выражается, обладают следующими общими свойствами:

1) Увеличение объема производства за счет роста затрат только по одному ресурсу имеет предел (нельзя нанимать много рабочих в одно помещение – не у всех будут места).

2) Факторы производства могут быть взаимодополняемы (рабочие и инструменты) и взаимозаменяемы (автоматизация производства).

Наиболее простой является двухфакторная модель производственной функции Кобба – Дугласа, с помощью которой раскрывается взаимосвязь труда (L) и капитала (К). Эти факторы взаимозаменяемы и взаимодополняемы.

2.Максимизация объема выпуска при ограничении на затраты.

Доходом (выручкой) R фирмы в определенном временном периоде называется произведение общего объема Х выпускаемой фирмой продукции на цену этой продукции.

Издержками С фирмы называют общие выплаты фирмы в определенном временном периоде за все виды затрат.

Прибылью фирмы П в определенном временном периоде называется разность между доходом и издержками.

Основная цель фирмы заключается в максимизации прибыли путем рационального распределения затрачиваемых ресурсов.

В случае долговременного промежутка фирма может свободно выбирать любой вектор 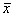затрат ресурсов, поэтому задача максимизации прибыли в случае долговременного промежутка имеет вид:

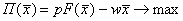
при условии х≥0

где р – цена единицы продукции, F(x) – производственная функция, выражающая связь между затратами ресурсов и выпуском,

w – цена единицы ресурса.

Это задача нелинейного программирования. Необходимые условия ее решения - равенство нулю частной производной.

Если в оптимальном решении использованы все ресурсы, то 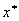>0.

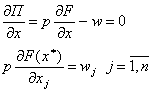
Отсюда следует, что в оптимальной точке стоимость предельного продукта данного ресурса должна равняться его цене.

Рассмотрим задачу с использованием двух видов ресурсов, т.е. 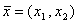. Тогда выручка R=pF(x₁,x₂); издержки C=w₁x₁+w₂x₂, и прибыль

П(x₁,x₂)= pF(x₁,x₂)- (w₁x₁+w₂x₂).

Линия уровня функции издержек производства называется изокостой. Ее уравнение w₁x₁+w₂x₂=const.

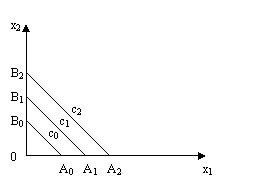
А₀В₀║ А₁В₁║ А₂В₂

с₀< с₁< с₂

А₀В₀: w₁x₁+w₂x₂=c₀

А₁В₁: w₁x₁+w₂x₂=c₁

А₂В₂: w₁x₁+w₂x₂=c₂

Решая эту задачу, получаем

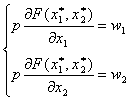
Вектор 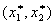затрат ресурсов, который является решением задачи, называется локальным рыночным равновесием фирмы в случае долговременного промежутка.

В данной системе разделим первое уравнение на второе, получим .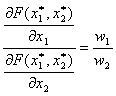

Отсюда следует: в точке 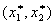локального рыночного равновесия фирмы отношение предельной производительности первого ресурса к предельной производительности второго ресурса равно отношению рыночных цен на эти ресурсы.

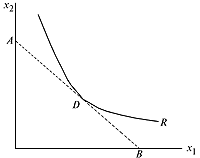
Здесь отрезок АВ есть изокоста, кривая R изокванта, касающаяся изокосты в точке D, которая и соответствует оптимальному набору ресурсов .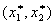

Левая часть выражения – это предельная норма замены первого ресурса вторым. Таким образом, в точке 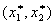локального рыночного равновесия фирмы предельная норма замены первого ресурса вторым равна отношению рыночных цен на эти ресурсы.

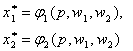
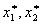- являются функциями от цен р, w₁, w₂. Эти выражения называются функциями спроса на ресурсы.

Подставив эти функции в ПФ: Х=F(x₁,x₂), получаем выражение .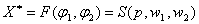

Это выражение называется функцией предложения выпуска.

3.Минимизация издержек при фиксированном объеме выпуска.

Выпуск фирмы задается производственной функцией Кобба-Дугласа: .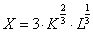

Стоимость аренды единицы фондов равна w_K=5 ус.ед./ед.ф, ставка зарплаты равна w_L=10 ус.ед./чел. На аренду фондов и оплату труда на фирме выделено С₀=150 ус.ед.

1. Определите максимальный выпуск фирмы и затраты труда и капитала при этом выпуске.

2. Дайте геометрическую интерпретацию полученного решения.

3. Вычислите прибыль фирмы при оптимальном выпуске.

4. Найдите предельную норму замены одного занятого работника капиталом в оптимальной точке.

Решение:

Издержки фирмы равны .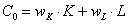

Составим математическую модель задачи.

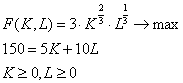
Для решения задачи применим метод Лагранжа. Составим функцию Лагранжа.

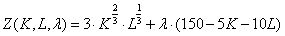
Найдем частные производные по каждой переменной. Воспользуемся формулами: .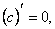

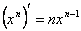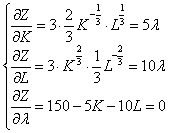(1)

Разделим первое уравнение на второе, получим:

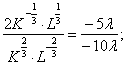
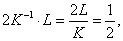откуда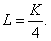

Подставим в функцию издержек, т.е. в третье уравнение системы.

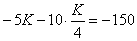
Тогда 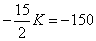, K=20.

Следовательно, L=5.

При этом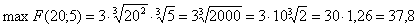

Геометрическая интерпретация:

Уравнение изокосты (линии постоянных издержек) .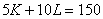

Строим на координатной плоскости прямую по двум точкам:

K	L

Уравнение изокванты (линии постоянных выпусков)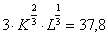

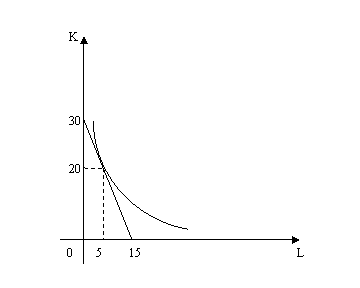
В оптимальной точке K=20, L=5 изокванта и изокоста касаются.

Для вычисления прибыли фирмы, найдем значения λ.

Рассмотрим одно из первых двух уравнений системы (1).

Например, .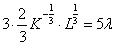

Выделим в левой части равенства производственную функцию F(K,L), для этого умножим и разделим ее на K.

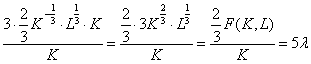
Отсюда .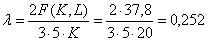

Из условия 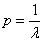, цена единицы продукции будет равна .

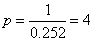Тогда прибыль фирмы определяется следующим образом:

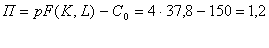
Прибыль очень мала, т.к. большие издержки.

Норма замены труда фондами определяется по формуле:

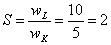, т.е. один работающий может быть заменен двумя единицами фондов.

1.Постановка задачи многокритериальной оптимизации.

В практической деятельности часто встречаются задачи, за­ключающиеся в поиске лучшего (оптимального) решения при наличии различных несводимых друг к другу критериев эф­фективности. Если такого рода задачи решаются методами математического программирования, то говорят о задачах многокритериальной оптимизации.

Многокритериальная оптимизация — это раздел математи­ческого программирования, посвященный проблемам выбора принципов оптимальности и методов нахождения их реализаций в экстремальных задачах с несколькими критериями.

Пусть на плоскости (х,у) задано множество ω и в каждой точке этого множества определены две непрерывные функции:

W₁=Φ(x,y) и W₂=Ψ(x,y).

Требуется найти точку 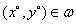, в которо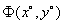й и 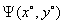принимают максимальные значения, т.е. решить совместно две экстремальные задач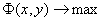и

и , .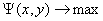

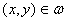В общем случае поставленная задача решения не имеет, удовлетворить обоим требованиям одновременно невозможно. И, следовательно, нужно искать какое-то компромиссное решение.

Среди известных методов решения задач многокритериальной оптимизации можно отметить:

1) метод последовательных уступок,

2) метод идеальной точки.

Оба метода используют множество Парето, составленное в данном случае из допустимых точек задачи, которые не могут быть «сдвинуты» в пределах допустимого множества с улучше­нием сразу по обоим критериям. Иными словами, улучшая значения одного из критериев, мы неизбежно ухудшаем значе­ния другого.