· Полигоном относительных частот (кратностей) дискретного вариационного ряда называется ломаная, соединяющая точки 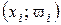 .
.
Замечание: Для интервального вариационного ряда в качестве абсциссы точки берут середину частичного интервала.
Полигон, построенный по дискретному вариационному ряду, является выборочным аналогом многоугольника распределения дискретной случайной величины. В первом приближении полигон указывает на вид теоретического распределения.
· Гистограммой относительных частот интервального вариационного ряда называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются интервалы разбиения 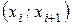 , а высотой – числа
, а высотой – числа 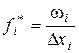 .
.
· Неотрицательное число 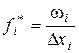 называется плотностью относительнойчастоты
называется плотностью относительнойчастоты 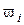 .
.
Каждый прямоугольник гистограммы имеет площадь, равную. Следовательно, вся площадь полученной фигуры будет равна 1.
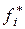 – статистический аналог дифференциальной функции распределения непрерывной СВ, и гистограмма, являясь статистическим аналогом кривой распределения, в первом приближении указывает на вид теоретического распределения.
– статистический аналог дифференциальной функции распределения непрерывной СВ, и гистограмма, являясь статистическим аналогом кривой распределения, в первом приближении указывает на вид теоретического распределения.
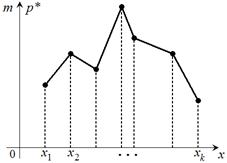 | 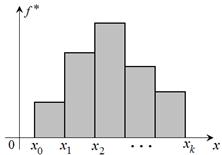 |
| Рис. 1. Полигон кратностей (частот) | Рис. 2. Гистограмма частот |
Если соединить середины верхних оснований прямоугольников отрезками, то получим полигон того же распределения, т. е. полигон повторяет контур гистограммы.
· Кумулятой называется кривая накопленных кратностей или относительных частот, которая представляет собой ломаную линию, соединяющую точки 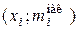 или
или 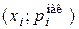
· Эмпирической функцией распределения называется функция 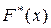 , задающая для каждого значения х частоту события
, задающая для каждого значения х частоту события 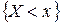 :
:
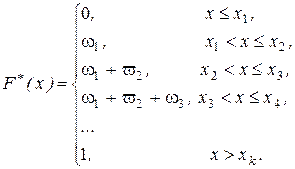
То есть значения эмпирической функции распределения естьнакопленные частоты.
Свойства эмпирической функции распределения:
1. Неубывающая.
2. Неотрицательная.
3. Область значения – 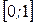 .
.
4. Если 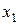 – наименьшая варианта, то для любых
– наименьшая варианта, то для любых 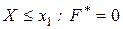 ;
;
если 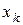 – наибольшая варианта, то для любых
– наибольшая варианта, то для любых 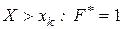 .
.
Для дискретного вариационного ряда эмпирическая функция распределения представляет собой разрывную ступенчатую функцию (рис. 4.) по аналогии с функцией распределения дискретной случайной величины.
Для интервального вариационного ряда имеем значения накопленных частот на концах интервалов. Поэтому для графического изображения этой функции в виде непрерывной линии целесообразно её доопределить, соединив точки графика, соответствующие концам интервалов, отрезками прямой. В результате полученная ломаная совпадёт с кумулятой (рис. 3).
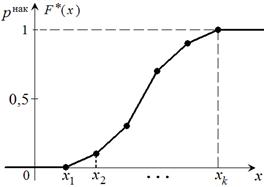 | 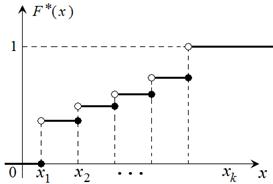 |
| Рис. 3. Кумулята относительных частот | Рис. 4. Эмпирическая функция дискретного вариационного ряда |
3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ВЫБОРКИ
· Модой 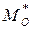 называется такое значение варианты, которой соответствует максимальное значение частоты.
называется такое значение варианты, которой соответствует максимальное значение частоты.
В случае интервального вариационного ряда на чертеже гистограммы мода находится внутри частичного интервала 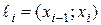 , которому соответствует наибольшая частота , которому соответствует наибольшая частота 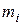 . Её значение вычисляется по формуле линейной интерполяции: . Её значение вычисляется по формуле линейной интерполяции: | 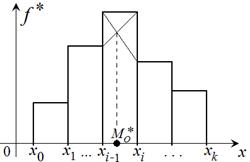 |
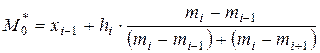 ,
,
где 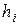 – длина частичного интервала
– длина частичного интервала 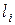 ,
,
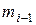 – частота, соответствующая предыдущему частичному интервалу
– частота, соответствующая предыдущему частичному интервалу 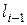 ,
,
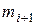 – частота, соответствующая следующему частичному интервалу
– частота, соответствующая следующему частичному интервалу 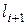 .
.
· Медианой 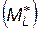 называется такое значение варианты
называется такое значение варианты 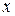 , для которой справедливы условия:
, для которой справедливы условия: 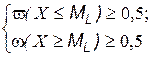
Медиана может быть приближённо найдена с помощью кумуляты (графика 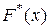 ), как значение признака, для которого ), как значение признака, для которого 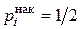 . Для интервального вариационного ряда прямая . Для интервального вариационного ряда прямая 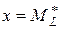 делит площадь гистограммы пополам. делит площадь гистограммы пополам. | 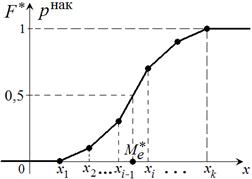 |
В случае интервального ряда медиана принадлежит тому частичному интервалу 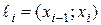 , для которого накопленная относительная частота составляет половину или больше половины всей суммы относительных частот, а предыдущая накопленная относительная частота меньше половины всей суммы относительных частот. Её значение вычисляется по формуле линейной интерполяции:
, для которого накопленная относительная частота составляет половину или больше половины всей суммы относительных частот, а предыдущая накопленная относительная частота меньше половины всей суммы относительных частот. Её значение вычисляется по формуле линейной интерполяции:
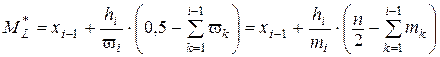
· Выборочной средней 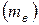 называется среднее арифметическое вариант:
называется среднее арифметическое вариант:
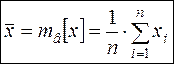
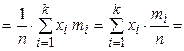 .
. 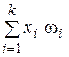 .
.
Выборочное среднее является статистическим аналогом математического ожидания случайной величины.
В случае интервального ряда в качестве 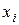 берутся середины частичных интервалов, т. е. значения
берутся середины частичных интервалов, т. е. значения 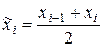 ,
, 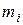 – соответствующие им частоты,
– соответствующие им частоты, 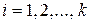 .
.
· Выборочной дисперсией 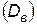 называется среднее арифметическое квадратов отклонений вариант от выборочной средней:
называется среднее арифметическое квадратов отклонений вариант от выборочной средней:
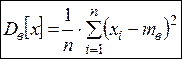
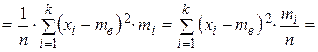
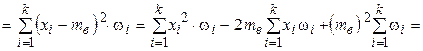
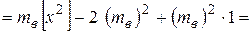
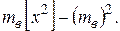
Выборочная дисперсия является статистическим аналогом дисперсии теоретического распределения.
· 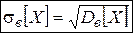 – выборочное среднее квадратическое отклонение.
– выборочное среднее квадратическое отклонение.
Среднее квадратическое отклонение является мерилом надёжности выборочной средней. Чем меньше квадратическое отклонение, тем лучше выборочная средняя отражает собой всю представляемую совокупность.
Для характеристики меры колеблемости изучаемого признака относительно выборочной средней служит коэффициент вариации: 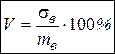 .
.
Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше.
В отличие от 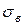 коэффициент вариации является безразмерной величиной, поэтому он пригоден для сравнения рассеяний вариационных рядов, варианты которых имеют различную размерность, например, если варианты одного ряда выражены в сантиметрах, а другого – в граммах.
коэффициент вариации является безразмерной величиной, поэтому он пригоден для сравнения рассеяний вариационных рядов, варианты которых имеют различную размерность, например, если варианты одного ряда выражены в сантиметрах, а другого – в граммах.
Если коэффициент вариации признака, принимающего только положительные значения, высок (например, более 100 %), то, как правило, это говорит о неоднородности значений признака.
· Выборочный начальный момент k–ого порядка: 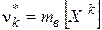 .
.
В частности: 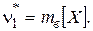
· Выборочный абсолютный начальный момент k–ого порядка: 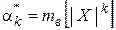
· Выборочный центральный момент k–ого порядка: 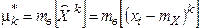
В частности: 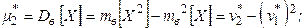
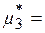
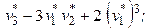
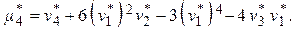
· Выборочный абсолютный центральный момент k–ого порядка:
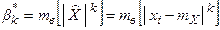
Среди моментов высших порядков особое значение имеют центральные моменты 3-го и 4-го порядка.
Нормальное распределение является одним из наиболее применяемых в математической статистике. Для оценки отклонения эмпирического распределения от нормального используют коэффициенты асимметрии и эксцесс, которые служат для сравнения полигона частот вариационного ряда с функцией плотности нормального распределения.
Выборочным коэффициентом асимметрии («скошенности») называется величина 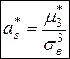 .
.
Выборочный коэффициент эксцесса («островершинности») определяется по формуле 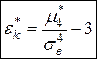 .
.
Эксцесс характеризует крутизну подъёма кривой распределения по сравнению с нормальной кривой. Для нормального распределения 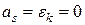 .
.
При отклонении от нормального распределения:
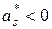 | – если «длинная» и более пологая часть кривой распределения расположена слева от соответствующей моде точки на оси абсцисс (рис. 5). |
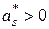 | – если часть кривой расположена справа от моды (рис. 6). |
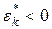 | – кривая имеет более низкую и пологую вершину (рис. 7). |
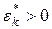 | – кривая имеет более высокую и острую вершину (рис. 7). |
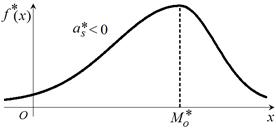 | 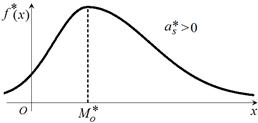 |
| Рис. 5 | Рис. 6 |
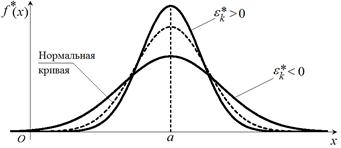 | |
| Рис. 7 |
 2015-03-20
2015-03-20 2364
2364








