Статистический ряд. Его первичная обработка

· Таблица, в которой содержатся номера опытов и соответствующие результаты измерений, называется статистическим рядом.

· Значение признака в i–ом опыте называется вариантой (xi).

· Кратностью или частотой 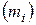варианты называется количество опытов, в которых наблюдалось одно и то же значение варианты. 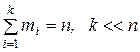(n – объём выборки)

· Относительной частотой варианты называется отношение кратности варианты к объёму выборки: .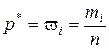

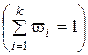Относительная частота является статистическим аналогом вероятности .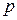

· Дискретным вариационным рядом называется упорядоченный (ранжированный) ряд различных значений признака (в порядке возрастания или убывания) и соответствующих им кратностей или частот.

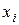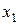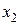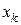			…		Σ
			…
			…

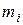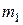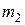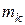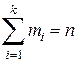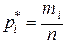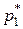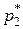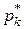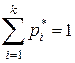Если объём выборки велик, интервал 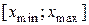, которому принадлежат все варианты, разбивается на частичные интервалы (чаще одинаковой длины).

Число интервалов k следует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака.

Число интервалов может быть определено по формуле Стерджеса: ,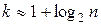

где 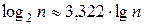, значение 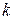подбирается целым.

Такой способ определения числа интервалов (1) является лишь рекомендуемым, но не обязательным.

Длина интервала находится по формуле: .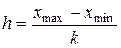

За начало первого частичного интервала, как правило (но не обязательно), выбирается точка .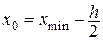

В первую строку таблицы интервального ряда вписывают частичные промежутки 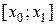, , 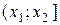…, , 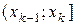имеющие одинаковую длину h, при этом весь интервал 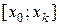должен полностью покрывать все имеющиеся значения признака, т. е. 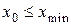, 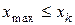. Во второй строке вписывают количество наблюдений 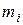(), попавших в каждый интервал. Таким образом, статистическое распределение примет вид:

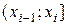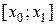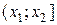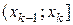			…		Σ
			…
			…

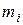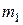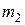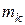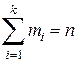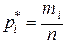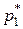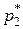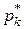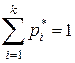· Интервальный вариационный ряд содержит интервалы разбиения и соответствующую им сумму кратностей или частот вариант, которые попали в данный интервал разбиения.

Накопленные кратности 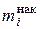(относительные частоты 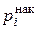) для каждого интервала находятся последовательным суммированием кратностей (относительных частот) всех предшествующих интервалов, включая данный. Накопленная кратность показывает, сколько наблюдалось вариантов со значением признака, меньшим чем х.