Метод эквивалентного преобразования схемы используют при расчете простых электрических цепей. В отдельных случаях имеется возможность применить его и для расчета сложных электрических цепей.
Суть метода эквивалентного преобразования схемы заключается в упрощении схемы, когда два (или несколько) однотипных элемента электрической цепи замещаются одним эквивалентным элементом того же типа. Под термином "эквивалентный элемент" подразумевается такой элемент, замещение на который не меняет значений токов и напряжений в остальной части электрической цепи.
Схематичный пример использования метода эквивалентного преобразования схемы для расчета сложной электрической цепи изображен ниже:
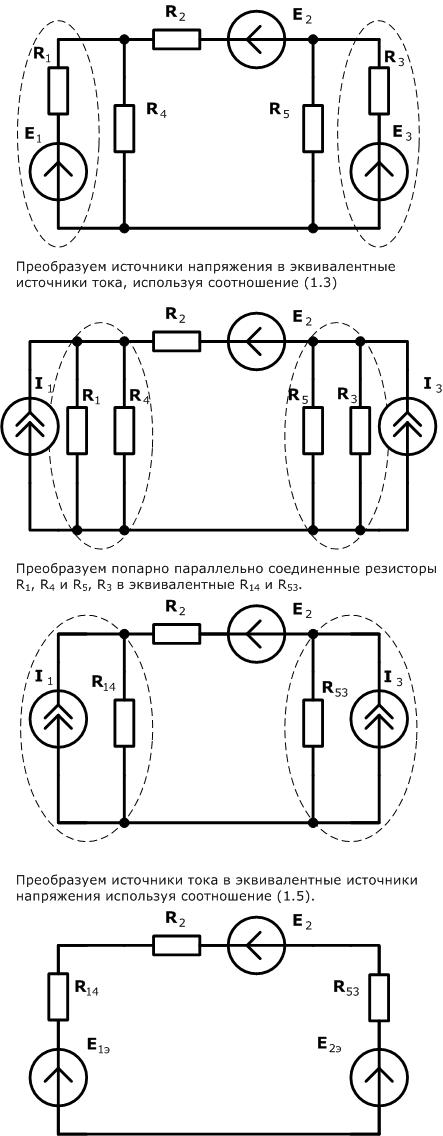
Например, после замены источника тока источником напряжения (рис. 1.3) в обобщенной ветви последняя будет выглядеть так:
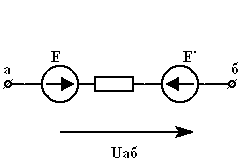 | = | 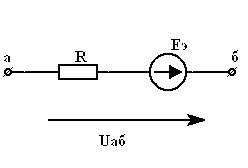 |
| Рис.3.1 | Рис.3.2 |
где 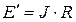 . Обратите внимание, направление эквивалентного источника ЭДС
. Обратите внимание, направление эквивалентного источника ЭДС 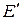 совпадает с напряжением источника тока
совпадает с напряжением источника тока 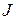 . Ниже будет показано, что данный участок цепи можно упростить, как показано на рис. (3.2), где
. Ниже будет показано, что данный участок цепи можно упростить, как показано на рис. (3.2), где 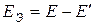 .
.
|
|
|
3.2. Последовательное соединение резисторов при эквивалентной замене суммируется:
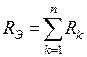 ,
,
где 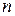 – число последовательно соединенных резисторов. При данном соединении
– число последовательно соединенных резисторов. При данном соединении 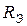 всегда больше большего из
всегда больше большего из 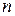 сопротивлений. В частном случае, если каждое из
сопротивлений. В частном случае, если каждое из 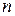 сопротивлений равно
сопротивлений равно 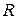 , то
, то 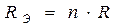 .
.
Пример. Определить эквивалентное сопротивление цепи на зажимах 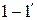 .
.
a)
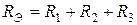 .
.
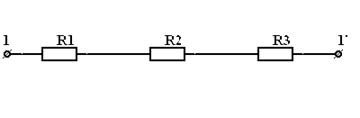 | = | 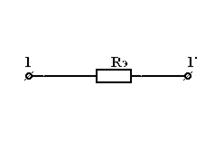 |
| Рис 3.4 | Рис 3.5 |
б)
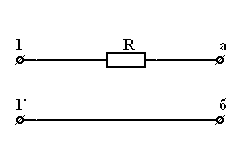 | 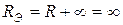 . . |
| Рис 3.6 |
Здесь 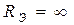 , т.к. разрыв цепи между точками
, т.к. разрыв цепи между точками 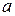 и
и 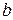 имеет бесконечно большое сопротивление.
имеет бесконечно большое сопротивление.
3.3. При параллельном соединении резистора суммируется их проводимость 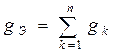 , где
, где 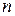 - число параллельно соединенных резисторов,
- число параллельно соединенных резисторов, 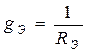 и
и 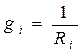 . При параллельном соединении
. При параллельном соединении 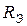 всегда меньше меньшего из
всегда меньше меньшего из 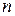 сопротивлений. В частном случае, если каждое из
сопротивлений. В частном случае, если каждое из 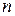 сопротивлений равно
сопротивлений равно 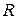 , то
, то 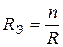 . В случае двух параллельно соединенных сопротивлений
. В случае двух параллельно соединенных сопротивлений 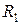 и
и 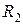 :
:
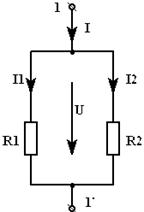 | = | 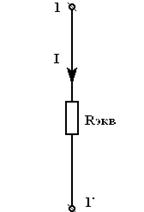 |
| Рис 3.7 | Рис 3.8 | |
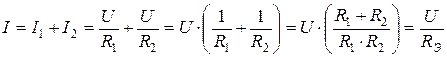 , , | ||
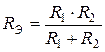 | или | 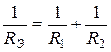 . . |
Пример. Определить 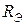 на зажимах
на зажимах 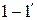 .
.
а)
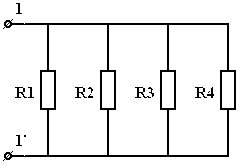 | = | 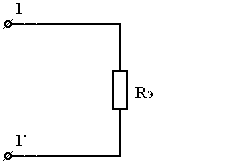 |
| Рис 3.9 | Рис 3.10 |
|
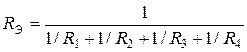 .
.
б)
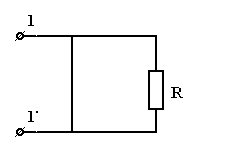 | 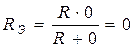 . . |
| Рис 3.10 |
Здесь 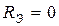 , т.к. сопротивление закоротки равно нулю.
, т.к. сопротивление закоротки равно нулю.
РАСЧЕТНЫЕ ФОРМУЛЫ
| Тип элемента | Последовательное соединение m-элементов | Параллельное соединение m-элементов |
| Резисторы | 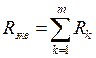 | 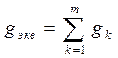 |
| Конденсаторы | 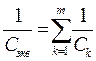 | 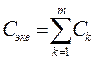 |
| Катушки индуктивности | 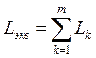 | 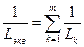 |
3.4. При смешанном соединении резисторов эквивалентное сопротивление 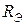 цепи определяет последовательным упрощением схемы и «сворачиванием» ее к одному сопротивлению, равному
цепи определяет последовательным упрощением схемы и «сворачиванием» ее к одному сопротивлению, равному 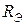 . При расчете токов в отдельных ветвях ЭЦ «разворачивают» в обратной последовательности.
. При расчете токов в отдельных ветвях ЭЦ «разворачивают» в обратной последовательности.
Пример. Определить 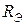 относительно зажимов
относительно зажимов 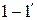 .
.
а)
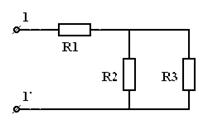 | = | 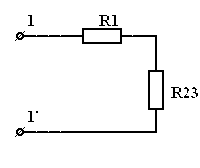 | = | 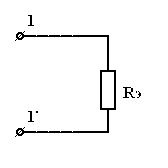 |
| Рис 3.11 | Рис 3.12 | Рис 3.12 |
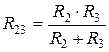 ,
, 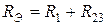
|
.
б)
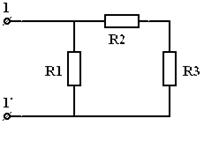 | = | 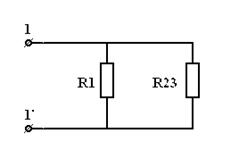 | = |  |
| Рис 3.13 | Рис 3.14 | Рис 3.15 |
|
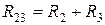 ,
, 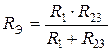 .
.
|
|
|
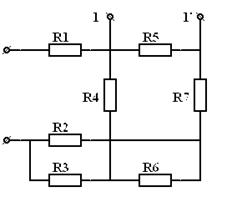 | = | 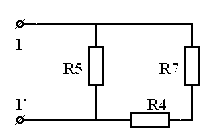 |
| Рис 3.16 | Рис 3.17 | |
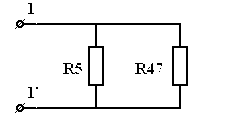 | = |  |
| Рис 3.18 | Рис 3.19 |
|
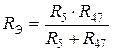 , где
, где 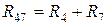 .
.
В последнем примере сопротивление 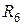 закорочено, а сопротивления
закорочено, а сопротивления 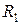 ,
, 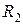 ,
, 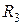 имеют только одну общую точку со схемой и поэтому они не учитываются. Сопротивления
имеют только одну общую точку со схемой и поэтому они не учитываются. Сопротивления 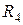 и
и 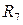 включены последовательно и эквивалентное им сопротивление
включены последовательно и эквивалентное им сопротивление 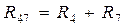 , а
, а 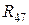 и
и 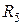 включены параллельно, поэтому:
включены параллельно, поэтому:
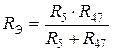 .
.
3.5. Преобразование пассивного треугольника сопротивлений в эквивалентную трехлучевую звезду. Схемы будут эквивалентны, если сопротивления между узлами 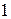 и
и 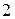 ,
, 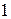 и
и 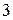 ,
, 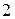 и
и 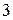 в обеих схемах «звезды» и «треугольника» будут одинаковыми:
в обеих схемах «звезды» и «треугольника» будут одинаковыми:
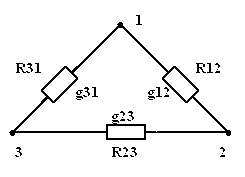 | = | 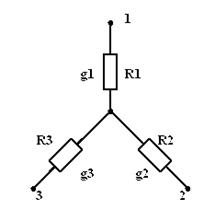 |
| Рис. 3.20 | Рис. 3.21 |
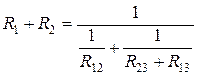 ,
, 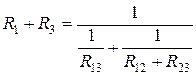 ,
, 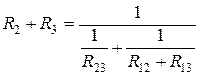 .
.
Решая совместно эти уравнения, получим:
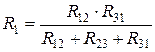 ,
, 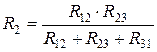 ,
, 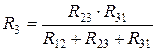 ,
,
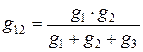 ,
, 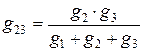 ,
, 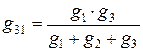 .
.
Обратное преобразование трехлучевой звезды в треугольник:
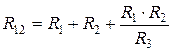 ,
, 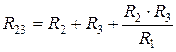 ,
, 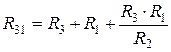 .
.
Пример. Определить эквивалентное сопротивление ЭЦ относительно зажимов 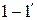 .
.
 | = | 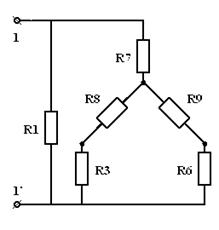 |
| Рис 3.22 | Рис 3.23 | |
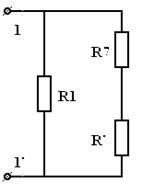 | = |  |
| Рис 3.24 | Рис 3.25 |
Сначала преобразуем треугольник сопротивлений 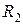 ,
, 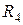 ,
, 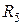 в эквивалентную трехлучевую звезду
в эквивалентную трехлучевую звезду 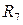 ,
, 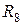 ,
, 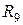 ; затем преобразуем последовательно соединенные резисторы
; затем преобразуем последовательно соединенные резисторы 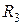 ,
, 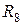 и
и 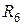 ,
, 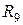 , эквивалентные сопротивления которых соединены между собой параллельно и могут быть заменены одним
, эквивалентные сопротивления которых соединены между собой параллельно и могут быть заменены одним 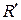 :
:
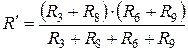 .
.
Резистор 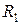 включен параллельно резисторам
включен параллельно резисторам 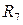 и
и 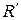 , соединенным между собой последовательно. Поэтому эквивалентное сопротивление всей ЭЦ относительно зажимов
, соединенным между собой последовательно. Поэтому эквивалентное сопротивление всей ЭЦ относительно зажимов 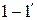 :
:
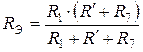 .
.
3.6. Преобразование ветвей, содержащих последовательные и параллельные соединения источников ЭДС и тока.
а)
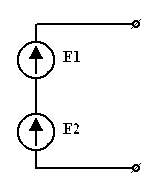 | = | 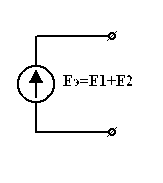 |
| Рис 3.26 | Рис 3.27 |
б)
 | = |  |
| Рис 3.28 | Рис 3.29 |
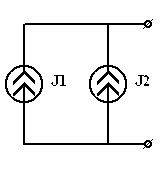
в)
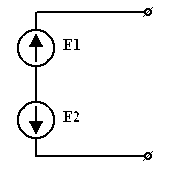 | = | 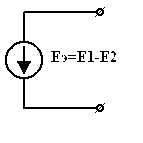 | или | 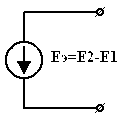 |
| Рис 3.30 | Рис 3.31 | Рис 3.32 |
|
г)
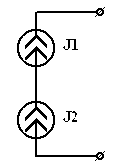 | Если 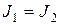 . Два источника тока могут быть соединены последовательно, если они равны и одинаково направлены в противном случае не будет выполняться ЗТК в месте соединения двух источников. . Два источника тока могут быть соединены последовательно, если они равны и одинаково направлены в противном случае не будет выполняться ЗТК в месте соединения двух источников. |
д)
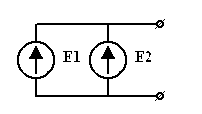 | 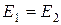 . Два источника ЭДС могут быть включены параллельно, если они равны и имеют одинаково включенную полярность. Если эти условия не выполняются, то ЗНК будет нарушен в контуре, содержащем эти источники. . Два источника ЭДС могут быть включены параллельно, если они равны и имеют одинаково включенную полярность. Если эти условия не выполняются, то ЗНК будет нарушен в контуре, содержащем эти источники. |
|
3.7. Часть схемы, состоящей из параллельных ветвей ЭДС 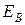 и проводимостями
и проводимостями 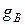 , эквивалентно либо одной ветви с проводимостью
, эквивалентно либо одной ветви с проводимостью 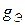 и ЭДС
и ЭДС 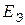 :
:
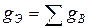 ,
, 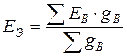 ,
,
либо двум параллельным ветвям с той же проводимостью 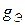 и источником тока
и источником тока 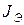 :
:
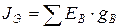 .
.
ПРАВИЛО ЗНАКОВ. Слагаемые 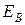 ,
, 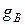 берутся с плюсом при совпадении направления ЭДС
берутся с плюсом при совпадении направления ЭДС 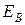 и
и 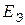 , при несовпадении – с минусом.
, при несовпадении – с минусом.
Пример. Преобразовать схему с параллельными ветвями, содержащими источники ЭДС, в эквивалентную.
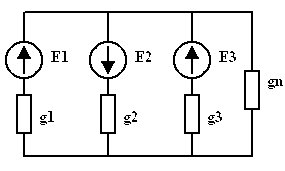 | = | 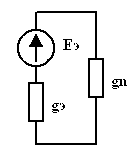 | = | 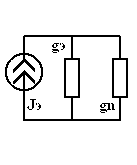 |
| Рис 3.33 | Рис 3.34 | Рис 3.35 |
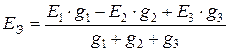 ,
, 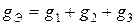 ,
, 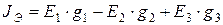 .
.
Пример.В заданной ЭЦ (рис.2.1) найти токи, используя эквивалентные преобразования.
Для начала преобразуем источник тока 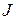 в источник напряжения:
в источник напряжения: 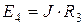 .
.
Заменим сопротивления 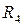 и
и 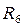 на эквивалентные
на эквивалентные 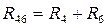 и
и 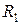 ,
, 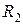 на
на 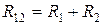 .
.
Элементы 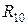 ,
, 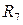 ,
, 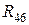 соединены в трехлучевую звезду, которую можно преобразовать в треугольник с сопротивлениями:
соединены в трехлучевую звезду, которую можно преобразовать в треугольник с сопротивлениями: 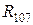 ,
, 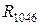 ,
, 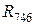 .
.
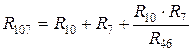 ,
, 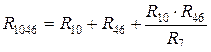 ,
, 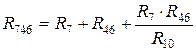 .
.
После преобразований схема приобретает вид:
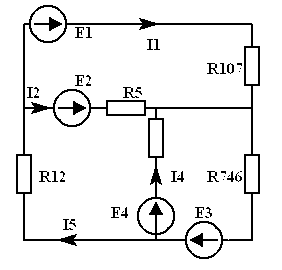 | Þ | 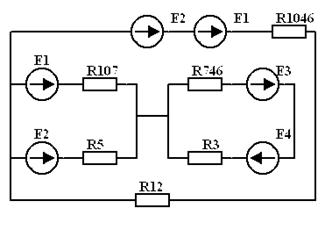 |
Последовательно упрощаем схему,
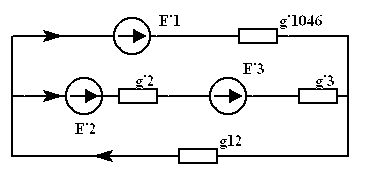 |  |
где
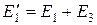 ,
, 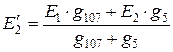 ,
, 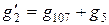 ,
,
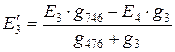 ,
, 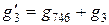 .
.
Схему 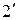 можно заменить на
можно заменить на 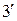 , где
, где
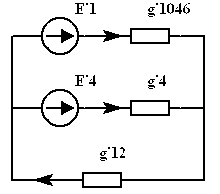 |  |
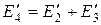 ,
, 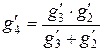 .
.
Заменяя 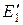 и
и 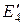 на эквивалентное
на эквивалентное 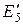 :
:
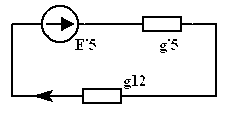 |  |
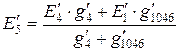 .
.
Тогда ток, протекающий через элементы 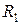 ,
, 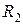 будет равен:
будет равен:
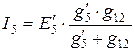 .
.
Токи, протекающие через 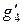 ,
, 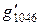 равны: (
равны: (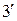 ):
):
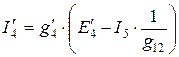 ,
, 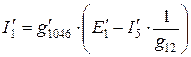 .
.
Посредством 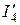 найдем токи на резисторах
найдем токи на резисторах 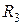 и
и 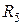 (
(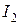 и
и 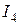 ):
):
1. 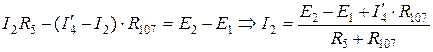 ,
,
1. 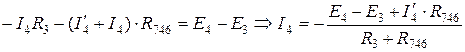 .
.
Остальные токи можно найти посредством ЗТК для изначальной схемы:
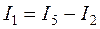 ,
, 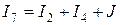 ,
, 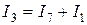 .
.
 2015-03-20
2015-03-20 47518
47518
